Zadanie nr 9633167
Narysuj dowolny trójkąt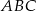 
a następnie skonstruuj trójkąt 
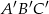podobny do trójkąta 
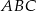w skali podobieństwa 
.
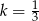Rozwiązanie
Na początek przypomnijmy sobie jak dzieli się konstrukcyjnie odcinek na trzy równe części.
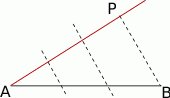
Jeżeli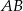 
jest danym odcinkiem, to dorysowujemy półprostą o początku w punkcie 
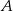, odkładamy na niej trzy odcinki równej długośći, koniec 
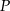ostatniego z nich łączymy z punktem 
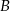, a przez końce pozostałych prowadzimy proste równoległe do 
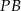. Na mocy twierdzenia Talesa, proste te podzielą dany odcinek na trzy równe części.
Korzystając z tej konstrukcji, łatwo jest skonstruować trójkąt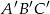 
.
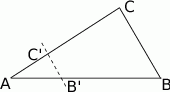
Wyznaczamy najpierw punkt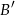 
na boku 
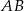tak, aby 
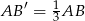. Potem prowadzimy przez niego prostą równoległą do 
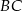. Jej punkt przecięcia z prostą 
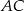daje nam 
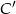. Oczywiście 
.
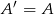