/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 22 marca 2014 Czas pracy: 170 minut
Zadania zamknięte
Dwadzieścia dziewcząt stanowi 62,5% uczniów klasy IB. Ilu chłopców jest w tej klasie?
A) 12 B) 6 C) 32 D) 9
Wszystkie liczby spełniające warunek 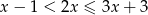 można zapisać za pomocą przedziału:
można zapisać za pomocą przedziału:
A) 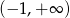 B)
B) 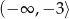 C)
C) 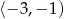 D)
D) 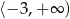
Liczba 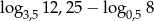 jest równa
jest równa
A) 5 B) 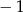 C)
C) 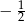 D) 1
D) 1
Rozwiązaniem układu równań 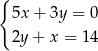 jest para
jest para 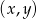 liczb takich, że
liczb takich, że
A) 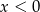 i
i 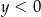 B)
B) 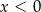 i
i 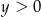 C)
C) 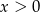 i
i 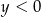 D)
D) 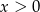 i
i 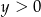
Wskaż zbiór rozwiązań nierówności 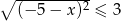 .
.
A) 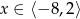 B)
B) 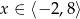 C)
C) 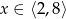 D)
D) 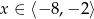
Wierzchołek paraboli o równaniu 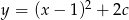 leży na prostej o równaniu
leży na prostej o równaniu 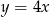 . Wtedy
. Wtedy
A) 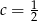 B)
B) 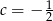 C)
C) 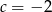 D)
D) 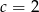
Kąt  jest ostry i
jest ostry i 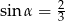 . Wartość wyrażenia
. Wartość wyrażenia 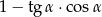 jest równa
jest równa
A) 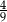 B)
B)  C)
C) 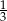 D)
D) 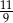
Wyrażenie 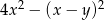 po rozłożeniu na czynniki przyjmuje postać:
po rozłożeniu na czynniki przyjmuje postać:
A) 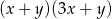 B)
B) 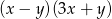 C)
C) 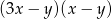 D)
D) 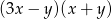
Liczba 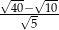 jest równa
jest równa
A) 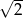 B)
B) 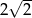 C) 4 D)
C) 4 D) 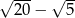
Liczba 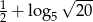 jest równa:
jest równa:
A) 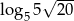 B)
B) 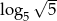 C)
C) 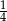 D)
D) 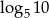
Na rysunku 1 przedstawiony jest wykres funkcji 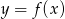 określonej dla
określonej dla 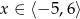 .
.
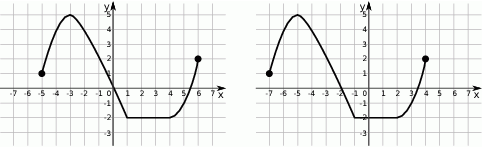
Rysunek 2 przedstawia wykres funkcji
A) 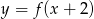 B)
B) 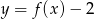 C)
C) 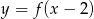 D)
D) 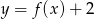
Z prostokąta 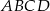 o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt 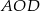 (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
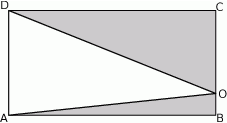
A) 7,5 B) 15 C) 20 D) 25
Ciąg 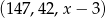 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 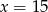 B)
B) 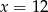 C)
C) 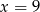 D)
D) 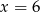
Ciągiem arytmetycznym jest ciąg o wyrazie ogólnym 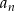 równym:
równym:
A) 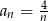 B)
B) 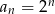 C)
C) 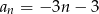 D)
D) 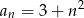
Liczba rzeczywistych rozwiązań równania 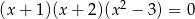 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
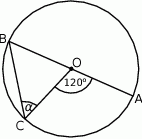
Punkt 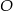 jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy 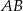 (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
A) 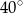 B)
B) 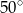 C)
C) 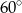 D)
D) 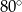
Który wyraz ciągu 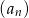 o wyrazie ogólnym
o wyrazie ogólnym 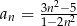 jest równy
jest równy 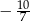 ?
?
A) piąty B) dwudziesty piąty C) siódmy D) dziewiąty
Poniżej zamieszczono fragment tabeli wartości funkcji liniowej
 | 1 | 2 | 4 |
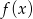 | 4 | 1 |
W pustym miejscu w tabeli powinna znajdować się liczba:
A) 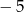 B) 5 C)
B) 5 C) 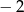 D) 2
D) 2
Dany jest trójkąt o wierzchołkach 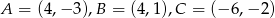 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 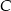 jest równa
jest równa
A) 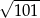 B)
B) 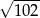 C)
C) 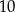 D)
D) 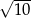
Prostokąt o bokach 3 i 5 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 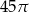 B)
B) 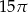 C)
C) 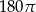 D)
D) 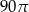
Średnia arytmetyczna zestawu danych: 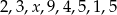 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 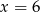 B)
B) 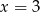 C)
C) 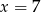 D)
D) 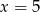
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy iloczyn oczek równy 4, wynosi
A) 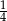 B)
B) 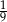 C)
C) 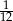 D)
D) 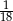
Kąt  jest ostry i
jest ostry i 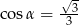 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 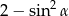 jest równa
jest równa
A) 0 B)  C)
C) 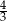 D) 1
D) 1
Równania 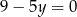 i
i 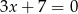 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe
B) są równoległe
C) przecinają się pod kątem 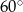
D) przecinają się pod kątem 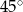
Zadania otwarte
Rozwiąż równanie 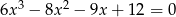 .
.
Oblicz wartość wyrażenia 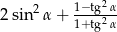 , gdzie
, gdzie  jest kątem ostrym.
jest kątem ostrym.
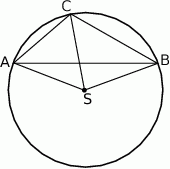
Punkt 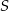 jest środkiem okręgu opisanego na trójkącie rozwartokątnym
jest środkiem okręgu opisanego na trójkącie rozwartokątnym 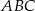 . Kąt
. Kąt 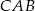 jest dwa razy większy od kąta
jest dwa razy większy od kąta 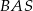 , a kąt
, a kąt 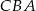 jest o
jest o 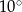 większy od kąta
większy od kąta 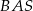 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 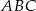 .
.
W tabeli przedstawiono oceny ze sprawdzianu z matematyki w klasie 1B.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 3 | 3 | 6 |  | 4 | 2 |
Średnia arytmetyczna tych ocen jest równa 3,48. Oblicz liczbę  ocen dobrych (4) otrzymanych przez uczniów na tym sprawdzianie.
ocen dobrych (4) otrzymanych przez uczniów na tym sprawdzianie.
Wykaż, że 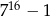 jest liczbą podzielną przez
jest liczbą podzielną przez 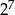 .
.
Wykaż, że jeżeli 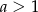 , to
, to 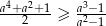 .
.
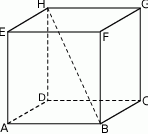
Podstawą graniastosłupa 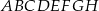 jest prostokąt
jest prostokąt 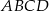 (zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta
(zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta 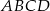 tworzy z jego krótszym bokiem kąt
tworzy z jego krótszym bokiem kąt 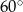 . Przekątna
. Przekątna 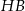 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 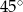 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
Punkty 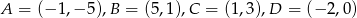 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 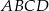 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Pole każdej z dwóch prostokątnych działek jest równe 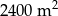 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.

