/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 8 marca 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 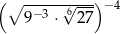 jest równa
jest równa
A) 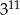 B)
B) 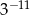 C)
C) 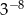 D)
D) 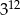
Gdy od 19% liczby 32 odejmiemy 16% liczby 19, to otrzymamy
A) 0 B) 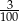 C) 3,04 D) 9,12
C) 3,04 D) 9,12
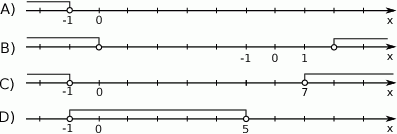
Zbiór rozwiązań nierówności 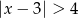 jest przedstawiony na rysunku
jest przedstawiony na rysunku
Zbiorem wartości funkcji 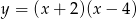 jest przedział
jest przedział
A) 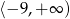 B)
B) 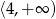 C)
C) 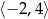 D)
D) 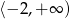
W trójkącie prostokątnym dane są kąty ostre: 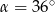 i
i 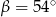 . Wtedy
. Wtedy 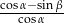 równa się
równa się
A) 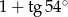 B)
B) 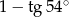 C) 1 D) 0
C) 1 D) 0
Liczby rzeczywiste 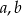 spełniają warunki:
spełniają warunki: 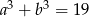 ,
, 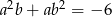 . Wtedy suma
. Wtedy suma 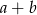 jest równa
jest równa
A) 37 B) 13 C) 1 D) 25
Dla każdej liczby rzeczywistej  , wyrażenie
, wyrażenie 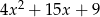 jest równe
jest równe
A) 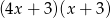 B)
B) 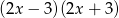 C)
C) 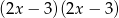 D)
D) 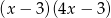
Zbiorem wartości funkcji 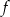 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
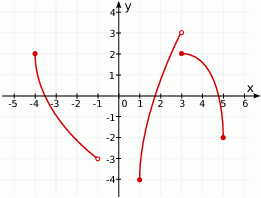
A) 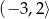 B)
B) 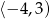 C)
C) 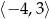 D)
D) 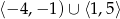
Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej 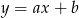 .
.
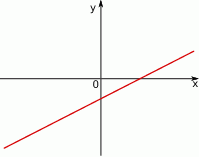
Jakie znaki mają współczynniki  i
i 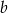 ?
?
A) 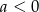 i
i 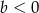 B)
B) 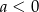 i
i 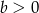 C)
C) 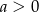 i
i 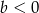 D)
D) 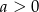 i
i 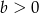
Liczba 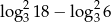 jest równa
jest równa
A) 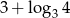 B)
B) 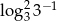 C)
C) 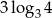 D)
D) 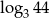
Punkt 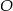 jest środkiem okręgu. Kąt
jest środkiem okręgu. Kąt  , zaznaczony na rysunku, ma miarę
, zaznaczony na rysunku, ma miarę
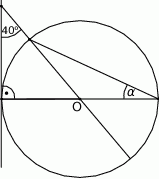
A) 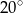 B)
B) 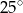 C)
C) 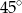 D)
D) 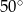
Najmniejszą liczbą całkowitą spełniającą nierówność 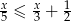 jest
jest
A) 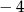 B)
B) 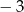 C)
C) 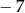 D)
D) 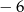
Która z podanych prostych jest symetryczna do prostej 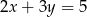 względem osi
względem osi 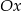 ?
?
A) 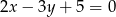 B)
B) 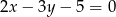 C)
C) 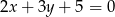 D)
D) 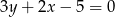
Punkt 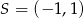 jest środkiem odcinka
jest środkiem odcinka 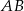 , gdzie
, gdzie 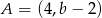 i
i 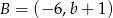 . Wówczas
. Wówczas
A) 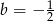 B)
B) 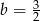 C)
C) 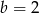 D)
D) 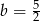
Pole powierzchni całkowitej sześcianu jest równe 48. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 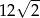 B)
B) 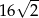 C)
C) 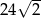 D)
D) 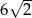
W ciągu arytmetycznym 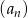 dane są:
dane są: 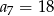 i
i 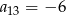 . Wtedy wyraz
. Wtedy wyraz 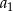 jest równy
jest równy
A) 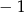 B)
B) 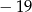 C) 29 D) 42
C) 29 D) 42
W ciągu geometrycznym 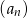 dane są
dane są 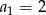 i
i 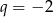 . Suma sześciu początkowych wyrazów tego ciągu jest równa
. Suma sześciu początkowych wyrazów tego ciągu jest równa
A) 86 B) 22 C) 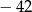 D) 42
D) 42
Boki równoległoboku mają długości: 6 cm i 10 cm, a jego pole wynosi 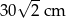 . Kąt ostry równoległoboku ma miarę:
. Kąt ostry równoległoboku ma miarę:
A) 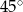 B)
B) 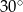 C)
C) 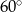 D)
D) 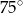
Przyprostokątne w trójkącie prostokątnym mają długości 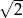 i
i 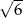 . Największy kąt ostry w tym trójkącie ma miarę
. Największy kąt ostry w tym trójkącie ma miarę
A) 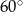 B)
B) 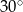 C)
C) 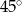 D)
D) 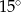
Odległość między środkami okręgów o równaniach 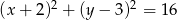 oraz
oraz 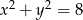 jest równa
jest równa
A) 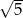 B)
B) 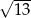 C) 13 D)
C) 13 D) 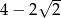
Pole powierzchni bocznej stożka o wysokości 12 i promieniu podstawy 5 jest równe
A) 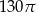 B)
B) 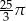 C)
C) 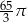 D)
D) 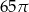
Ciąg 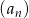 jest określony wzorem
jest określony wzorem 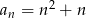 , dla
, dla 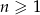 . Który wyraz tego ciągu jest równy 30?
. Który wyraz tego ciągu jest równy 30?
A) drugi B) trzeci C) piąty D) szósty
Ze zbioru dzielników naturalnych liczby 8 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 4 jest równe
A) 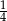 B)
B) 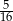 C)
C)  D)
D) 
Zadania otwarte
Rozwiąż nierówność 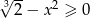 .
.
Kąt  jest ostry i
jest ostry i 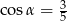 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
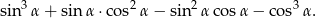
Nieskończony ciąg geometryczny 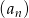 jest określony wzorem
jest określony wzorem 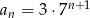 , dla
, dla 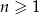 . Oblicz iloraz
. Oblicz iloraz 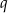 tego ciągu.
tego ciągu.
Wykaż, że liczba 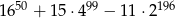 jest podzielna przez 13.
jest podzielna przez 13.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 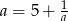 , to
, to 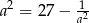 .
.
Wyznacz najmniejszą i największą wartość funkcji 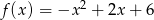 w przedziale
w przedziale 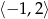 .
.
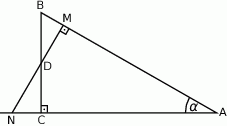
Przez środek 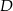 przyprostokątnej
przyprostokątnej 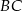 trójkąta prostokątnego
trójkąta prostokątnego 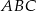 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 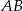 . Prosta ta przecina proste
. Prosta ta przecina proste 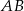 i
i 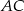 odpowiednio w punktach
odpowiednio w punktach 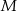 i
i 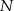 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 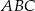 i
i 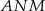 jest równa
jest równa 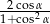 .
.
Pole podstawy stożka jest równe 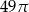 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 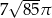 . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
W kartonach rozmieszczono 2800 metalowych puszek w ten sposób, że w każdym kartonie znajduje się ta sama liczba puszek. Gdyby do każdego kartonu włożyć o 15 puszek mniej, to należałoby użyć o 60 kartonów więcej. W ilu kartonach rozmieszczono puszki?
Oblicz długość cięciwy, którą wycina z prostej 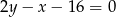 okrąg o środku w punkcie
okrąg o środku w punkcie 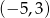 i promieniu 5.
i promieniu 5.

