/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 1 marca 2014 Czas pracy: 180 minut
Rozwiąż nierówność 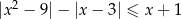 .
.
Która liczba jest większa 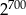 , czy
, czy 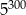 ?
?
Dany jest trójkąt 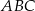 , w którym
, w którym 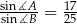 . Na boku
. Na boku 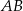 leży punkt
leży punkt 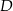 taki, że
taki, że 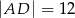 ,
, 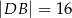 oraz
oraz 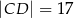 . Oblicz długość promienia okręgu opisanego na trójkącie
. Oblicz długość promienia okręgu opisanego na trójkącie 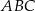 .
.
Rozwiąż równanie 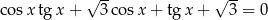 w zbiorze
w zbiorze 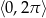 .
.
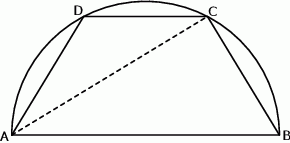
W półkole o promieniu  wpisano trapez równoramienny o przekątnej długości
wpisano trapez równoramienny o przekątnej długości 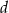 . Oblicz długość krótszej podstawy trapezu.
. Oblicz długość krótszej podstawy trapezu.
Pierwszy, trzeci i trzynasty wyraz ciągu arytmetycznego 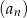 ,
, 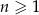 są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu
są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu 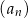 jest równy 27. Wyznacz wzór ciągu
jest równy 27. Wyznacz wzór ciągu 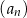 wiedząc, że nie jest to ciąg stały.
wiedząc, że nie jest to ciąg stały.
Suma reszt jakie otrzymujemy dzieląc wielomian 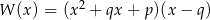 przez dwumiany
przez dwumiany 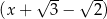 i
i 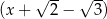 jest równa
jest równa 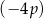 , gdzie
, gdzie 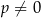 . Oblicz
. Oblicz 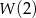 .
.
Z punktu 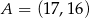 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 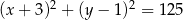 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Wykaż, że jeżeli 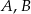 są podzbiorami
są podzbiorami 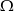 oraz
oraz 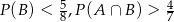 , to
, to 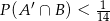 (
(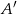 oznacza zdarzenie przeciwne do
oznacza zdarzenie przeciwne do 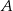 ).
).
Oblicz, ile jest dziewięciocyfrowych liczb naturalnych parzystych, w zapisie których każda z cyfr: 5 i 3 występuje dokładnie 3 razy.
Podstawą ostrosłupa 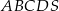 jest prostokąt
jest prostokąt 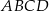 o bokach długości
o bokach długości  i
i 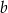 . Krawędź
. Krawędź 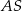 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 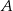 od krawędzi
od krawędzi 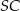 jest równa
jest równa 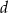 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
Wyznacz największy wyraz ciągu 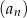 danego wzorem
danego wzorem 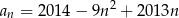 , dla
, dla 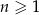 .
.

