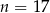Zadanie nr 8636705
Wyznacz wszystkie liczby naturalne  spełniające równanie
spełniające równanie
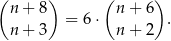
Rozwiązanie
Korzystamy ze wzorów
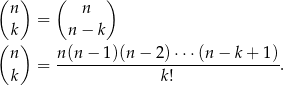
Mamy zatem
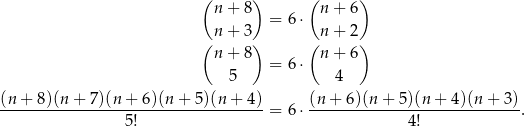
Skracamy teraz obie strony przez 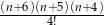 i otrzymujemy:
i otrzymujemy:
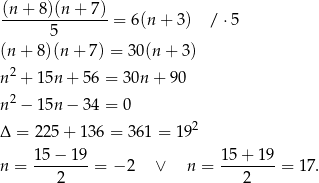
Ujemne rozwiązanie odrzucamy i mamy 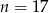 .
.
Odpowiedź: 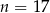
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby naturalne  spełniające równanie
spełniające równanie
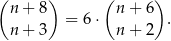
Korzystamy ze wzorów
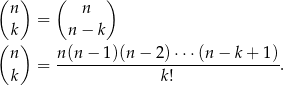
Mamy zatem
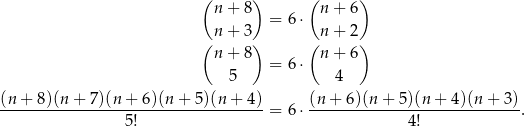
Skracamy teraz obie strony przez 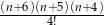 i otrzymujemy:
i otrzymujemy:
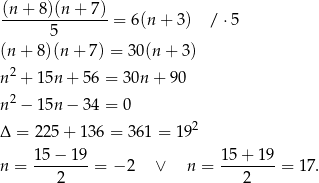
Ujemne rozwiązanie odrzucamy i mamy 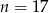 .
.
Odpowiedź: