/Szkoła średnia/Kombinatoryka/Symbol Newtona

Zadanie nr 9332547

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 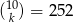10 (k) = 252 .

Rozwiązanie

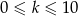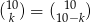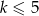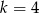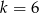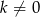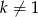Oczywiście szukamy liczby całkowitej 0 ≤ k ≤ 10 . Ponieważ 10 10 ( k) = (10−k) , możemy założyć, że k ≤ 5 – jeżeli wyjdzie nam np. k = 4 , to na koniec dołożymy też rozwiązanie k = 6 . Jest też jasne, że k ⁄= 0 i k ⁄= 1 . Mamy zatem 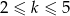2 ≤ k ≤ 5 . Teraz tak naprawdę można po prostu sprawdzić te pozostałe 4 wartości 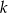k (licząc symbol Newtona). My jednak postaramy się być odrobinę mądrzejsi. Przekształćmy dane równanie

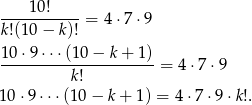
10! -----------= 4 ⋅7⋅9 k!(10− k)! 10 ⋅9⋅⋅ ⋅(10− k+ 1) ---------k-!--------- = 4 ⋅7⋅ 9 10⋅ 9⋅⋅⋅(1 0− k + 1) = 4⋅7 ⋅9 ⋅k!.

Liczba z lewej strony dzieli się przez 5, więc przez 5 musi się też dzielić prawa strona, co w połączeniu z naszym założeniem 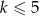k ≤ 5 , daje 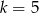k = 5 . Sprawdźmy, że wtedy jest OK.

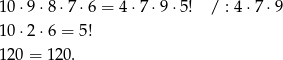
10⋅9 ⋅8 ⋅7 ⋅6 = 4 ⋅7⋅ 9⋅5! / : 4⋅7 ⋅9 10⋅2 ⋅6 = 5! 120 = 120 .

 
Odpowiedź: k = 5

Wersja PDF