/Gimnazjum/Egzamin gimnazjalny/Egzamin 2014/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 5 kwietnia 2014 Czas pracy: 90 minut
Do pustej szklanki wlano 3 miarki syropu.
Ile takich samych miarek wody należy dolać do szklanki, aby syrop stanowił 30% napoju? Wybierz odpowiedź spośród podanych.
A) 10 B) 5 C) 6 D) 7
W pewnej hurtowni za 120 jednakowych długopisów i 360 jednakowych ołówków zapłacono 600 zł. Jaka byłaby cena zakupu 170 takich samych długopisów i 510 takich samych ołówków w tej hurtowni? Wybierz odpowiedź spośród podanych.
A) 850 zł B) 800 zł C) 780 zł D) 680 zł
Informacja do zadań 3 i 4
Zaczynając od punktu 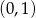 budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 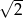 .
.
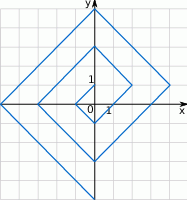
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli  jest liczbą parzystą, to odcinek o numerze jest liczbą parzystą, to odcinek o numerze  jest równoległydo odcinka o numerze 3. jest równoległydo odcinka o numerze 3. | P | F |
Jeżeli  jest liczbą nieparzystą, to długość odcinka o numerze jest liczbą nieparzystą, to długość odcinka o numerze  jest równa jest równa 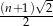 . . | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Łamana złożona z 8 początkowych odcinków ma długość 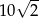 . . | P | F |
Długość setnego odcinka jest równa 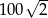 . . | P | F |
Ile spośród liczb: 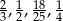 spełnia warunek
spełnia warunek 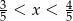 ?
?
Wybierz odpowiedź spośród podanych.
A) Jedna liczba. B) Dwie liczby. C) Trzy liczby. D) Cztery liczby.
Do pudełka włożono piłki zielone i czerwone. Wszystkich piłek jest 8, a piłek czerwonych jest 6.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia czerwonej piłki jest trzy razy większe, niż prawdopodobieństwo wyciągnięcia piłki zielonej. | P | F |
| Jeśli z pudełka zabierzemy 2 czerwone piłki, to prawdopodobieństwa wyciągnięcia piłki czerwonej i zielonej będą równe. | P | F |
Dane są liczby  i
i 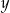 spełniające warunki:
spełniające warunki: 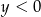 i
i 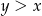 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  jest ujemna. jest ujemna. | P | F |
Liczba  jest większa od liczby jest większa od liczby 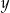 . . | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 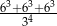 jest równa
jest równa
A) 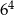 B)
B) 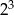 C)
C) 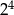 D)
D) 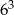
Informacja do zadań 9 – 11
Wykres przedstawia zależność ilości paliwa pozostałego w baku samochodu (w litrach) od liczby przejechanych kilometrów.
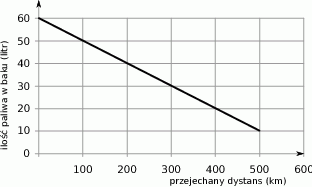
Ile paliwa pozostało w baku po przejechaniu 300 km? Wybierz odpowiedź spośród podanych.
A) 50 litrów B) 40 litrów C) 30 litrów D) 20 litrów
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Samochód spalił połowę początkowej ilości paliwa po przejechaniu 250 km. | P | F |
| Gdyby początkowo w baku było 40 litrów paliwa, to samochód mógłby przejechać 500 km. | P | F |
Ile paliwa potrzebuje ten samochód, aby przejechać 15 km? Wybierz odpowiedź spośród podanych.
A) 2 litry B) 1,5 litra C) 3 litry D) 2,5 litra
Liczby uczestników konkursu ortograficznego z klas pierwszych, drugich i trzecich gimnazjum są do siebie w proporcji 11 : 12 : 9.
Jaki procent uczestników konkursu stanowili drugoklasiści? Wybierz odpowiedź spośród podanych.
A) 60% B) 35% C) 37,5% D) 50%
Pociąg towarowy pokonał trasę o długości 360 km w czasie 4,5 godziny.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Gdyby średnia prędkość pociągu była większa o 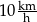 , to pociąg pokonałby tę trasę w czasie o 30 minut krótszym. , to pociąg pokonałby tę trasę w czasie o 30 minut krótszym. | P | F |
| Gdyby pociąg poruszał się z tą samą prędkością średnią, to trasę długości 450 km przebyłby w czasie 5,5 godziny. | P | F |
Basen ogrodowy, o wymiarach podanych na rysunku, wypełniono wodą do  jego wysokości.
jego wysokości.
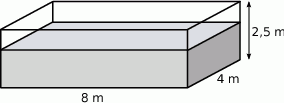
Ile litrów wody jest w basenie?
Wybierz odpowiedź spośród podanych.
A) 48 000 litrów B) 480 000 litrów C) 4 800 litrów D) 480 litrów
Punkt 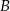 jest środkiem okręgu. Prosta
jest środkiem okręgu. Prosta 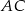 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 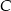 ,
, 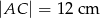 i
i 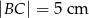 .
.
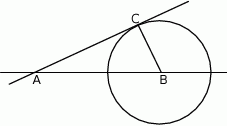
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Długość odcinka 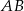 jest równa
jest równa
A) 3 cm B) 9 cm C) 14 cm D) 13 cm
W prostokątnym układzie współrzędnych umieszczono figurę przedstawioną na rysunku.
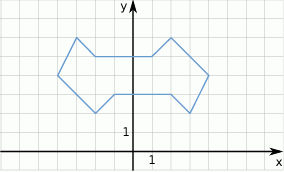
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Przedstawiona figura
A) posiada jedną oś symetrii
B) posiada dwie osie symetrii
C) posiada jeden środek symetrii
D) posiada dwa środki symetrii
Na rysunkach I, II i III dane są trzy trójkąty.
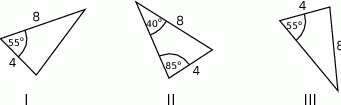
Na których rysunkach trójkąty są przystające? Wybierz odpowiedź spośród podanych.
A) I i II B) I i III C) II i III D) I, II i III
W trapezie 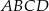 podstawa
podstawa 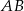 jest dłuższa od podstawy
jest dłuższa od podstawy 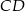 .
.
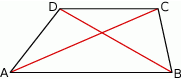
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 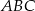 jest równe połowie pola trapezu jest równe połowie pola trapezu 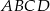 . . | P | F |
Suma pól trójkątów 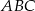 i i 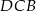 jest równa polu trapezu. jest równa polu trapezu. | P | F |
Na siatce sześcianu zaznaczono jego dwie ściany 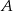 i
i 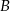 oraz jego dwie krawędzie
oraz jego dwie krawędzie 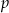 i
i 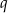 .
.
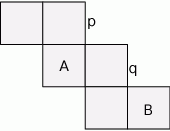
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ściany 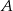 i i 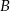 są przeciwległymi ścianami sześcianu. są przeciwległymi ścianami sześcianu. | P | F |
Krawędzie 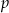 i i 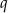 są prostopadłymi krawędziami sześcianu. są prostopadłymi krawędziami sześcianu. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli średnicę podstawy stożka zwiększymy 3 razy, a jego wysokość zmniejszymy 3 razy, to objętość stożka
A) zwiększy się dziewięciokrotnie.
B) zmniejszy się trzykrotnie.
C) zwiększy się trzykrotnie.
D) nie zmieni się.
Jacek miał wziąć udział w obozie narciarskim, ale zachorował i zamiast niego na obóz pojechał jego dwa razy starszy brat. Ta zamiana spowodowała, że średnia wieku uczestników obozu wzrosła o rok. Oblicz, ile lat ma Jacek, jeżeli w obozie wzięło udział 12 osób. Zapisz obliczenia.
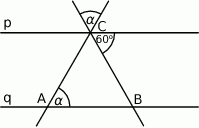
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt 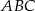 . Prosta
. Prosta 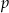 jest równoległa do prostej
jest równoległa do prostej 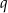 oraz przechodzi przez punkt
oraz przechodzi przez punkt 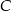 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 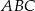 jest równoboczny.
jest równoboczny.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 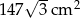 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 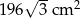 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.

