/Gimnazjum/Egzamin gimnazjalny/Egzamin 2014/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 22 marca 2014 Czas pracy: 90 minut
W pewnym sklepie za 18 bułek należy zapłacić 12,6 zł.
Ile bułek można kupić w tym sklepie za 17,5 zł, przy tej samej cenie za jedną bułkę? Wybierz odpowiedź spośród podanych.
A) 28 B) 25 C) 24 D) 20
Trzy pompy o jednakowej wydajności pracując jednocześnie, wypompowały wodę zgromadzoną w zbiorniku w czasie 24 godzin.
Ile takich pomp należałoby użyć, aby tę samą ilość wody wypompować w ciągu 8 godzin? Wybierz odpowiedź spośród podanych.
A) 9 B) 8 C) 6 D) 12
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 16848 jest liczbą podzielną przez 32. | P | F |
| Liczba 16848 jest wielokrotnością 81. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Wyrażenie 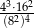 ma wartość
ma wartość
A) 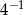 B)
B) 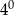 C)
C) 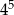 D)
D) 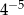
Która z liczb nie spełnia warunku 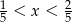 ?
?
Wybierz odpowiedź spośród podanych.
A) 0,3 B) 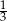 C)
C) 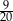 D)
D) 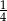
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Cena filmu na płycie DVD po 20% obniżce wynosi 52 zł. Cena tego filmu przed obniżką była równa
A) 65 zł. B) 64 zł. C) 62,4 zł. D) 60 zł.
Dane są liczby  i
i 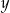 spełniające warunki:
spełniające warunki: 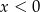 i
i 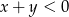 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 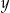 musi być ujemna. musi być ujemna. | P | F |
Liczby  i i 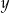 mogą być równe. mogą być równe. | P | F |
Organizatorzy loterii fantowej przygotowali zestaw losów, w którym były dwa rodzaje losów: niebieskie i zielone. Losów niebieskich było dwa razy mniej niż losów zielonych i upoważniały one do odbioru cenniejszej nagrody. Uczestnicy loterii losowali po jednym losie, który po wylosowaniu był usuwany z zestawu. Pierwszy uczestnik loterii wyciągnął los niebieski, a drugi uczestnik wyciągnął los zielony.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez trzecią osobę losu niebieskiego jest równe 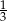 . . | P | F |
Prawdopodobieństwo wyciągnięcia przez pierwszą osobę losu zielonego było równe  . . | P | F |
Informacja do zadań 9 – 11
W ramach prac konserwacyjnych opróżniono z wody zbiornik retencyjny. Wykres przedstawia zależność ilości pozostałej w zbiorniku wody (w 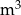 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach).
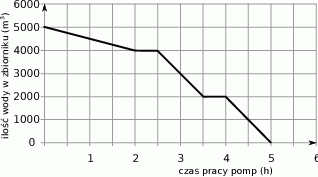
Jaka była średnia prędkość opróżniania całego zbiornika? Wybierz odpowiedź spośród podanych.
A) 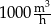 B)
B) 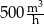 C)
C) 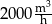 D)
D) 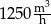
W trakcie wypompowywania wody nastąpiły dwie przerwy i w trakcie jednej z nich zwiększono wydajność pomp. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Łączny czas trwania przerw wyniósł 120 minut. | P | F |
| Wydajność pomp zwiększono w czasie pierwszej przerwy. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po 3,5 h wypompowano ze zbiornika połowę wody. | P | F |
Po 1 h wypompowano ze zbiornika 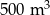 wody. wody. | P | F |
Do okręgu o środku  należą punkty
należą punkty  i
i  . Okrąg ma długość 72, a łuk
. Okrąg ma długość 72, a łuk  ma długość 15.
ma długość 15.
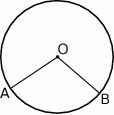
Jaką miarę ma kąt środkowy oparty na tym łuku?
Wybierz odpowiedź spośród podanych.
A) 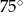 B)
B) 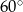 C)
C) 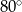 D)
D) 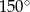
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga 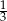 jego wysokości.
jego wysokości.
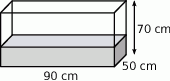
Ile litrów wody jest w akwarium?
Wybierz odpowiedź spośród podanych.
A) 105000 litrów B) 105 litrów C) 1050 litrów D) 10500 litrów
Punkt 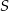 jest środkiem okręgu wpisanego w romb
jest środkiem okręgu wpisanego w romb 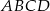 . Okrąg ten jest styczny do boku
. Okrąg ten jest styczny do boku 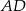 w punkcie
w punkcie 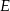 oraz
oraz 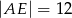 ,
, 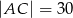 .
.
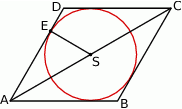
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Promień 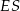 okręgu ma długość
okręgu ma długość
A) 12 B) 9 C) 8 D) 6
Średnia prędkość samochodu na trasie przebytej w czasie 3 godzin wyniosła 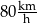 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Aby czas przejazdu był o 1 godzinę krótszy, średnia prędkość samochodu na tej trasie musiałaby wynosić 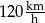 . . | P | F |
Gdyby średnia prędkość samochodu na tej trasie była równa 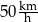 , to czas przejazdu byłby równy 5 godzin. , to czas przejazdu byłby równy 5 godzin. | P | F |
W trójkącie równoramiennym 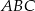 , w którym
, w którym 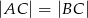 i
i 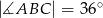 poprowadzono wysokość
poprowadzono wysokość  i dwusieczną kąta
i dwusieczną kąta 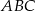 przecinającą bok
przecinającą bok 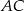 w punkcie
w punkcie 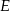 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 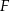 .
.
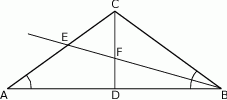
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
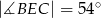 | P | F |
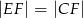 | P | F |
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
Na którym rysunku trójkąty nie są przystające? Wybierz odpowiedź spośród podanych.
A) I B) II C) III D) IV
Metalową kulę o objętości 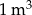 przetopiono na kulki o objętości
przetopiono na kulki o objętości 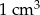 , a następnie otrzymane kulki ustawiono obok siebie w jednej linii tak jak na rysunku.
, a następnie otrzymane kulki ustawiono obok siebie w jednej linii tak jak na rysunku.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W wyniku opisanego przetopienia otrzymano 1 000 000 małych kulek. | P | F |
Długość 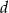 otrzymanej linii kulek jest równa 20 km. otrzymanej linii kulek jest równa 20 km. | P | F |
Siatka ostrosłupa składa się z kwadratu i czterech trójkątów prostokątnych zbudowanych na bokach tego kwadratu.
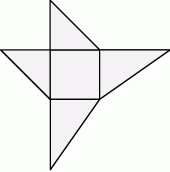
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość tego ostrosłupa jest równa długości jednej z jego krawędzi. | P | F |
| Wszystkie wysokości ścian bocznych tego ostrosłupa mają taką samą długość. | P | F |
Kształt i wymiary drewnianej deseczki przedstawiono na rysunku.
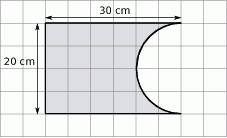
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Powierzchnia tej deseczki (w 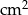 ) jest równa
) jest równa
A) 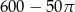 B)
B) 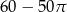 C)
C) 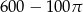 D)
D) 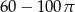
W pewnej klasie liczba chłopców stanowi 75% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze czterech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
Obwód trapezu równoramiennego jest równy 56 cm, ramię ma długość 15 cm, a różnica długości podstaw wynosi 18 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.

