/Szkoła średnia/Zadania maturalne/Matura 2014/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 3 czerwca 2014 Czas pracy: 170 minut
Zadania zamknięte
Która z poniższych równości jest prawdziwa dla każdej liczby rzeczywistej  ?
?
A) 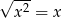 B)
B) 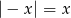 C)
C) 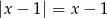 D)
D) 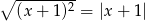
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział największego inwestora?
A) 12% B) 32% C) 48% D) 52%
Dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 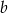 wyrażenie
wyrażenie 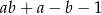 jest równe
jest równe
A) 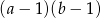 B)
B) 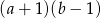 C)
C) 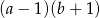 D)
D) 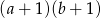
Na prostej o równaniu 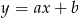 leżą punkty
leżą punkty 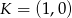 i
i 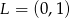 . Wynika stąd, że
. Wynika stąd, że
A) 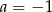 i
i 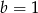 B)
B) 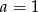 i
i 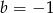 C)
C) 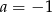 i
i 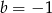 D)
D) 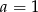 i
i 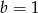
Dane są liczby: 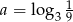 ,
, 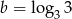 ,
, 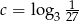 . Który z poniższych warunków jest prawdziwy?
. Który z poniższych warunków jest prawdziwy?
A) 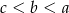 B)
B) 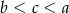 C)
C) 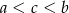 D)
D) 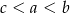
Funkcja 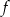 jest określona wzorem
jest określona wzorem 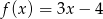 dla każdej liczby z przedziału
dla każdej liczby z przedziału 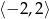 . Zbiorem wartości tej funkcji jest przedział
. Zbiorem wartości tej funkcji jest przedział
A) 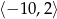 B)
B) 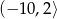 C)
C) 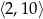 D)
D) 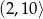
Jednym z miejsc zerowych funkcji kwadratowej 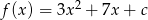 jest liczba
jest liczba 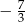 . Wówczas
. Wówczas  jest równe
jest równe
A) 0 B) 1 C) 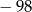 D) 98
D) 98
Liczba 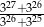 jest równa
jest równa
A) 1 B) 3 C) 6 D) 9
Dane są wielomiany: 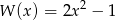 ,
, 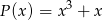 ,
, 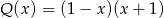 . Stopień wielomianu
. Stopień wielomianu 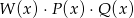 jest równy
jest równy
A) 3 B) 6 C) 7 D) 12
Pierwsza współrzędna wierzchołka paraboli o równaniu 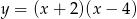 jest równa
jest równa
A) 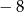 B)
B) 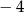 C) 1 D) 2
C) 1 D) 2
W ciągu geometrycznym 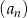 , określonym dla
, określonym dla 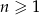 , wyraz
, wyraz 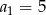 , natomiast iloraz
, natomiast iloraz 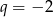 . Suma dziesięciu początkowych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych wyrazów tego ciągu jest równa
A) 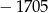 B)
B) 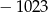 C) 1705 D) 5115
C) 1705 D) 5115
W ciągu arytmetycznym 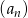 , określonym dla
, określonym dla 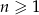 , dane są dwa wyrazy:
, dane są dwa wyrazy: 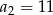 i
i 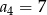 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 36 B) 40 C) 13 D) 20
Miara kąta  spełnia warunek:
spełnia warunek: 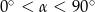 . Wyrażenie
. Wyrażenie 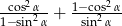 jest równe
jest równe
A) 1 B) 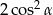 C) 2 D)
C) 2 D) 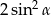
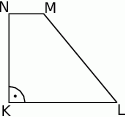
W trapezie 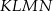 , w którym
, w którym 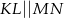 , kąt
, kąt 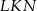 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 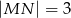 ,
, 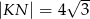 ,
, 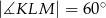 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
A) 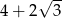 B)
B) 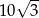 C)
C) 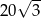 D)
D) 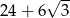
Średnia arytmetyczna liczby punktów uzyskanych na egzaminie przez studentów I grupy, liczącej 40 studentów, jest równa 30. Dwudziestu studentów tworzących II grupę otrzymało w sumie 1800 punktów. Zatem średni wynik z tego egzaminu, liczony łącznie dla wszystkich studentów z obu grup, jest równy
A) 20 pkt B) 30 pkt C) 50 pkt D) 60 pkt
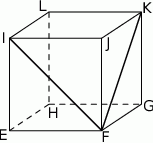
W sześcianie 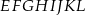 poprowadzono z wierzchołka
poprowadzono z wierzchołka 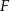 dwie przekątne sąsiednich ścian,
dwie przekątne sąsiednich ścian, 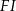 oraz
oraz 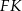 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 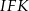 jest równa
jest równa
A) 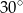 B)
B) 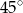 C)
C) 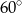 D)
D) 
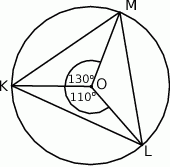
Punkt 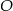 jest środkiem okręgu (zobacz rysunek). Miara kąta
jest środkiem okręgu (zobacz rysunek). Miara kąta 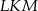 jest równa
jest równa
A) 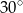 B)
B) 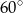 C)
C) 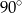 D)
D) 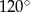
Na trójkącie prostokątnym, którego przyprostokątne mają długości 12 i 9, opisano okrąg. Promień tego okręgu jest równy
A) 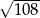 B)
B) 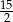 C) 15 D)
C) 15 D) 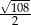
Ze zbioru kolejnych liczb naturalnych 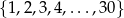 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 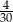 B)
B) 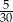 C)
C) 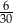 D)
D) 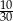
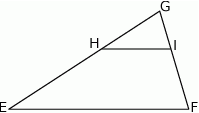
W trójkącie 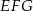 bok
bok 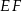 ma długość 21. Prosta równoległa do boku
ma długość 21. Prosta równoległa do boku 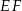 przecina boki
przecina boki 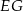 i
i 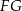 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 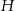 oraz
oraz 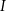 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 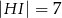 i
i 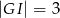 . Wtedy długość odcinka
. Wtedy długość odcinka 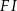 jest równa
jest równa
A) 6 B) 9 C) 12 D) 17
Na planie miasta, narysowanym w skali 1:20 000, park jest prostokątem o bokach 2 cm i 5 cm. Stąd wynika, że ten park ma powierzchnię
A) 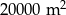 B)
B) 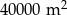 C)
C) 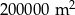 D)
D) 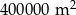
Proste o równaniach: 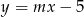 i
i 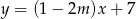 są równoległe, gdy
są równoległe, gdy
A) 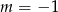 B)
B) 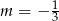 C)
C) 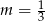 D)
D) 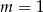
Punkty 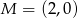 i
i 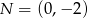 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 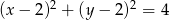
B) 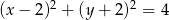
C) 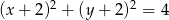
D) 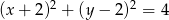
Objętość walca o promieniu podstawy 4 jest równa 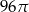 . Pole powierzchni bocznej tego walca jest równe
. Pole powierzchni bocznej tego walca jest równe
A) 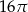 B)
B) 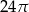 C)
C) 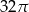 D)
D) 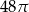
Objętość ostrosłupa prawidłowego czworokątnego jest równa 432, a krawędź podstawy tego ostrosłupa ma długość 12. Wysokość tego ostrosłupa jest równa
A) 3 B) 9 C) 27 D) 108
Zadania otwarte
Rozwiąż nierówność 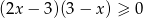 .
.
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 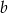 prawdziwa jest nierówność
prawdziwa jest nierówność
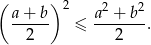
Kąt  jest ostry oraz
jest ostry oraz 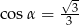 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 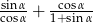 .
.
Liczby 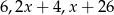 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Dane są dwa podzbiory zbioru liczb całkowitych:
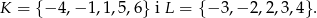
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
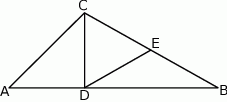
Dany jest trójkąt 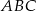 . Odcinek
. Odcinek 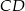 jest wysokością tego trójkąta, punkt
jest wysokością tego trójkąta, punkt 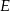 jest środkiem boku
jest środkiem boku 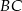 (tak jak na rysunku) i
(tak jak na rysunku) i 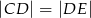 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 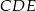 jest równoboczny.
jest równoboczny.
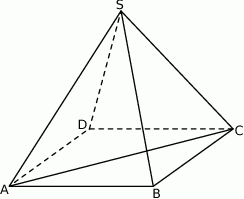
W ostrosłupie prawidłowym czworokątnym 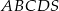 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 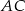 podstawy ma długość
podstawy ma długość 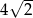 . Kąt
. Kąt 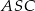 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 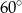 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Trasę etapu wyścigu kolarskiego o długości 150 km pan Nowak pokonał w czasie o 1 godzinę i 50 minut krótszym niż jego kolega z drużyny, pan Kowalski. Średnia wartość prędkości, z jaką pan Nowak jechał na tym etapie, była o 11 km/h większa od średniej wartości prędkości pana Kowalskiego na tej trasie. Oblicz średnie wartości prędkości, z jakimi przejechali całą trasę obaj zawodnicy.
Podstawą trójkąta równoramiennego 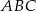 jest bok
jest bok 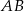 , gdzie
, gdzie 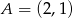 i
i 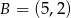 . Ramię tego trójkąta zawiera się w prostej o równaniu
. Ramię tego trójkąta zawiera się w prostej o równaniu 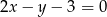 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 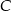 .
.

