/Szkoła średnia/Zadania maturalne/Matura 2014/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 3 czerwca 2014 Czas pracy: 180 minut
Rozwiąż nierówność 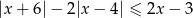 .
.
W czworokąt 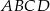 , w którym
, w którym 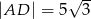 i
i 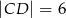 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 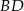 tworzy z bokiem
tworzy z bokiem 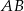 czworokąta kąt o mierze
czworokąta kąt o mierze 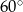 , natomiast z bokiem
, natomiast z bokiem 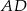 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy 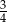 . Wyznacz długości boków
. Wyznacz długości boków 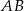 i
i 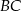 oraz długość przekątnej
oraz długość przekątnej 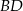 tego czworokąta.
tego czworokąta.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 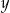 prawdziwa jest nierówność
prawdziwa jest nierówność
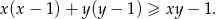
Rozwiąż nierówność 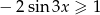 w przedziale
w przedziale 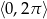 .
.
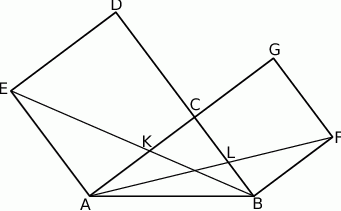
Na przyprostokątnych 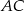 i
i 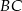 trójkąta prostokątnego
trójkąta prostokątnego 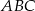 zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 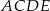 i
i 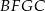 . Odcinek
. Odcinek 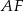 przecina przyprostokątną
przecina przyprostokątną 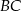 w punkcie
w punkcie 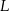 , a odcinek
, a odcinek 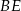 przecina przyprostokątną
przecina przyprostokątną 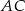 w punkcie
w punkcie 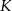 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 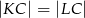 .
.
Wyznacz wszystkie wartości parametru 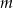 , dla których równanie
, dla których równanie 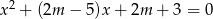 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 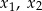 takie, że
takie, że 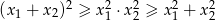 .
.
Odcinek 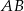 o długości 4 jest zawarty w prostej o równaniu
o długości 4 jest zawarty w prostej o równaniu 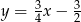 . Symetralna odcinka
. Symetralna odcinka 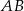 przecina oś
przecina oś 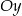 w punkcie
w punkcie 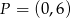 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 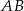 .
.
Trzy liczby są kolejnymi wyrazami ciągu geometrycznego, którego iloraz jest różny od 1. Jeżeli weźmiemy kolejno drugą z nich, pierwszą i trzecią, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Jeżeli pierwszy wyraz tego ciągu arytmetycznego zmniejszymy o 7, drugi pozostawimy bez zmian, a trzeci zwiększymy o 3, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz te liczby.
Reszta z dzielenia wielomianu 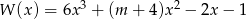 przez dwumian
przez dwumian 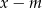 jest równa 8. Oblicz wartość
jest równa 8. Oblicz wartość 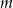 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Podstawą ostrosłupa jest kwadrat 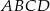 o boku długości 25. Ściany boczne
o boku długości 25. Ściany boczne 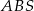 i
i 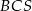 mają takie same pola, każde równe 250. Ściany boczne
mają takie same pola, każde równe 250. Ściany boczne 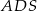 i
i 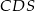 też mają jednakowe pola, każde równe 187,5. Krawędzie boczne
też mają jednakowe pola, każde równe 187,5. Krawędzie boczne 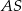 i
i 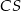 mają równe długości. Oblicz objętość tego ostrosłupa.
mają równe długości. Oblicz objętość tego ostrosłupa.
W urnie jest dziesięć kul: 4 białe, 3 czarne, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród wylosowanych kul nie ma kul w tym samym kolorze. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

