/Szkoła średnia/Funkcje

Zadanie nr 1047681

Dodaj do ulubionych
Dodaj do rozwiązanych

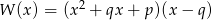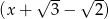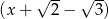Suma reszt jakie otrzymujemy dzieląc wielomian 2 W (x) = (x + qx + p)(x − q ) przez dwumiany √ -- √ -- (x + 3 − 2) i √ -- √ -- (x + 2 − 3) jest równa 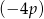(− 4p) , gdzie 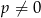p ⁄= 0 . Oblicz W (2) .

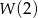Rozwiązanie

Przekształćmy najpierw wzór danego wielomianu.

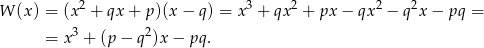
2 3 2 2 2 W (x) = (x + qx+ p)(x − q) = x + qx + px − qx − q x − pq = = x3 + (p− q2)x− pq.

Reszta z dzielenia wielomianu 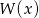W (x ) przez dwumian 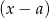(x − a) to po prostu 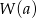W (a) . Jeżeli oznaczymy 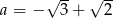√ -- √ -- a = − 3 + 2 , to wiemy, że

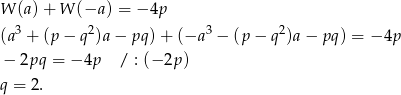
W (a)+ W (−a ) = − 4p 3 2 3 2 (a + (p − q )a− pq )+ (−a − (p − q )a− pq ) = − 4p − 2pq = − 4p / : (− 2p) q = 2.

W takim razie

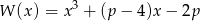
3 W (x ) = x + (p − 4)x − 2p

i

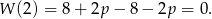
W (2) = 8 + 2p − 8 − 2p = 0.

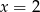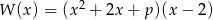(Mogliśmy też wstawić x = 2 do pierwotnego wzoru W (x ) = (x2 + 2x + p)(x − 2) .)  
Odpowiedź: W (2 ) = 0

Wersja PDF