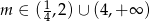/Szkoła średnia/Funkcje

Zadanie nr 1333914

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 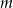m funkcja 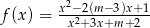x2−2(m−3)x+1- f(x ) = x2+3x+m +2 jest określona dla każdego 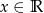x ∈ R i ma dwa różne miejsca zerowe?

Rozwiązanie

Sprawdźmy najpierw kiedy mianownik nie ma miejsc zerowych (aby dziedziną był zbiór 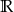R )

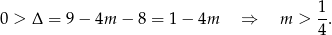
0 > Δ = 9 − 4m − 8 = 1 − 4m ⇒ m > 1. 4

Miejsca zerowe funkcji 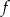f to dokładnie miejsca zerowe licznika. Aby funkcja 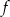f miała dwa różne miejsca zerowe musi być Δ > 0 .

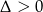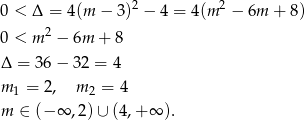
2 2 0 < Δ = 4(m − 3) − 4 = 4(m − 6m + 8) 0 < m 2 − 6m + 8 Δ = 36 − 32 = 4 m = 2, m 2 = 4 1 m ∈ (− ∞ ,2)∪ (4 ,+ ∞ ).

 
Odpowiedź: m ∈ (1,2) ∪ (4,+ ∞ ) 4

Wersja PDF