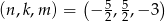/Szkoła średnia/Funkcje

Zadanie nr 1581087

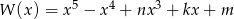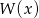Dany jest wielomian 5 4 3 W (x) = x − x + nx + kx+ m . Wyznacz wszystkie wartości parametrów n,k,m dla których reszta z dzielenia wielomianu W (x ) przez wielomian 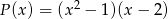P(x ) = (x2 − 1)(x− 2) jest równa R(x) = x− 4 .

Wersja PDF

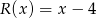Rozwiązanie

Zauważmy najpierw, że

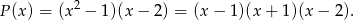
2 P(x) = (x − 1)(x− 2) = (x − 1)(x + 1)(x − 2 ).

Podana reszta z dzielenia wielomianu 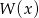W (x) przez wielomian 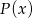P(x ) oznacza, że

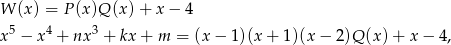
W (x) = P(x)Q (x) + x − 4 x5 − x4 + nx 3 + kx + m = (x − 1)(x+ 1)(x− 2)Q (x)+ x − 4,

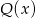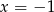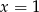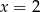dla pewnego wielomianu Q (x) . Podstawiamy teraz w tej równości kolejno x = − 1 , x = 1 i x = 2 . Otrzymujemy układ równań

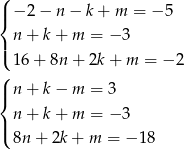
( | − 2 − n − k + m = − 5 { | n + k + m = − 3 ( 16 + 8n + 2k+ m = − 2 ( |{ n + k − m = 3 n + k + m = − 3 |( 8n + 2k + m = −1 8

Dodajemy do drugiego trzeciego równania pierwsze (żeby skrócić 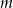m ) i mamy

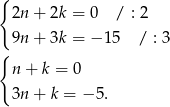
{ 2n + 2k = 0 / : 2 9n + 3k = − 15 / : 3 { n + k = 0 3n + k = −5 .

Odejmujemy teraz od drugiego równania pierwsze (żeby skrócić 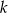k ) i mamy

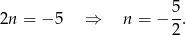
2n = − 5 ⇒ n = − 5. 2

Stąd 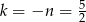k = −n = 52 i

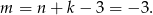
m = n + k− 3 = − 3.

 
Odpowiedź: ( ) (n ,k ,m) = − 52, 52,− 3

Wersja PDF