/Szkoła średnia/Funkcje

Zadanie nr 1614453

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz największą wartość wielomianu 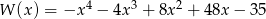4 3 2 W (x) = −x − 4x + 8x + 48x − 35 .

Rozwiązanie

Liczymy pochodną.

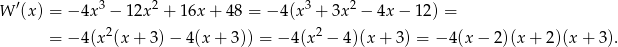
′ 3 2 3 2 W (x) = − 4x − 12x + 1 6x+ 48 = − 4(x + 3x − 4x − 12) = = − 4(x2(x + 3 )− 4(x + 3)) = − 4(x2 − 4)(x + 3) = − 4(x − 2 )(x+ 2)(x+ 3).

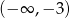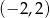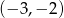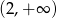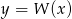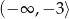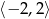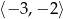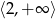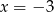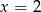Widać teraz, że pochodna jest dodatnia na przedziałach: (− ∞ ,− 3) , (− 2,2 ) oraz ujemna na przedziałach: (−3 ,−2 ) , (2,+ ∞ ) . To oznacza, że funkcja y = W (x) rośnie na przedziałach (−∞ ,− 3⟩ , ⟨− 2,2⟩ oraz maleje na przedziałach ⟨− 3,− 2⟩ , ⟨2,+ ∞ ⟩ . W szczególności, w punktach x = − 3 i x = 2 są maksima lokalne i dla jednego z tych argumentów funkcja 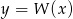y = W (x) przyjmuje swoją największą wartość. Ponieważ

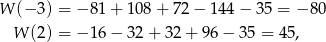
W (− 3) = − 81 + 108 + 72 − 1 44− 35 = − 80 W (2) = − 16 − 32 + 32 + 96 − 35 = 45,

największa wartość funkcji to 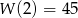W (2) = 45 .

Na koniec dla ciekawskich wykresy funkcji 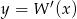y = W ′(x) i y = W (x) .

PIC

 
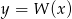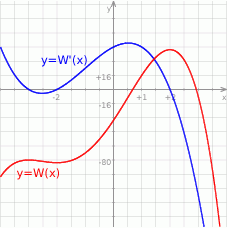
Odpowiedź: Wmax = W (2) = 45

Wersja PDF