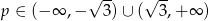Zadanie nr 1907485
Funkcja homograficzna jest określona wzorem 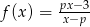 gdzie
gdzie 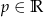 i
i 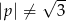 .
.
- Dla
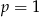 zapisz wzór funkcji w postaci
zapisz wzór funkcji w postaci 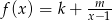 , gdzie
, gdzie 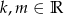 .
. - Wyznacz wszystkie wartosci
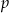 , dla których w przedziale
, dla których w przedziale 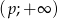 funkcja jest malejąca.
funkcja jest malejąca.
Rozwiązanie
- Przekształcamy
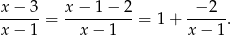
Odpowiedź: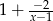
- Zapiszmy wzór funkcji w postaci kanonicznej (jak w poprzednim podpunkcie).
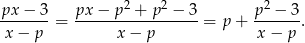
Po pierwsze zauważmy, że licznik 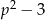 musi być dodatni, bo inaczej funkcja zbiegając do
musi być dodatni, bo inaczej funkcja zbiegając do 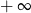 byłaby rosnąca (jak
byłaby rosnąca (jak 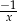 ). Przy tym założeniu funkcja ta jest malejąca na przedziale
). Przy tym założeniu funkcja ta jest malejąca na przedziale 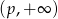 , bo jest przesunięciem funkcji
, bo jest przesunięciem funkcji 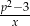 o wektor
o wektor ![[p,p ]](https://img.zadania.info/zad/1907485/HzadR8x.gif) .
.
Dla ciekawskich przykładowy wykres dla 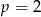 .
.
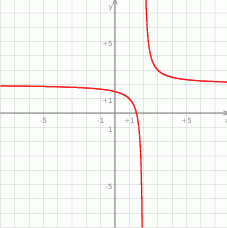
Odpowiedź: