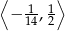/Szkoła średnia/Funkcje

Zadanie nr 2163784

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz zbiór wartości funkcji określonej wzorem: 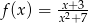-x+3 f (x) = x2+7 dla x ∈ R .

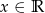Rozwiązanie

Sposób I

Musimy ustalić dla jakich wartości parametru 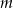m równanie

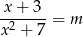
x + 3 -------= m x 2 + 7

ma rozwiązania. Liczymy.

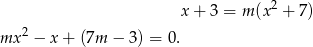
2 x + 3 = m(x + 7) mx 2 − x + (7m − 3) = 0 .

Zauważmy teraz, że jeżeli 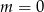m = 0 , to mamy równanie 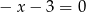− x− 3 = 0 , które oczywiście ma rozwiązania. Jeżeli natomiast 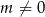m ⁄= 0 , to mamy równanie kwadratowe, więc wystarczy sprawdzić, kiedy Δ ≥ 0 .

2 0 ≤ Δ = 1 − 4m (7m − 3) = − 28m + 12m + 1 /⋅ (−1 ) 0 ≥ 28m 2 − 12m − 1 2 Δ = 144 + 1 12 = 256 = 16 12− 16 4 1 12 + 16 28 1 m 1 = --------= − --- = − ---, m 2 = --------= ---= -- ⟨ 56 ⟩ 5 6 14 56 56 2 m ∈ − -1-, 1 . 14 2

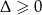Sposób II

Zauważmy, że

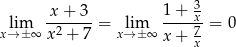
-x+--3- 1-+-3x- xl→im±∞ x2 + 7 = xl→im±∞ 7 = 0 x + x

oraz

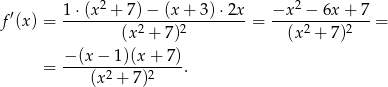
2 2 f ′(x ) = 1-⋅(x-+--7)−--(x+--3)⋅2x- = −x---−-6x-+--7 = (x2 + 7)2 (x2 + 7)2 − (x − 1)(x + 7) = ------2-----2---. (x + 7)

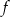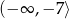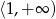W takim razie funkcja f maleje na przedziałach (− ∞ ,− 7⟩ i ⟨1,+ ∞ ) . Ponadto rośnie na przedziale ⟨− 7,1 ⟩ .

PIC

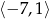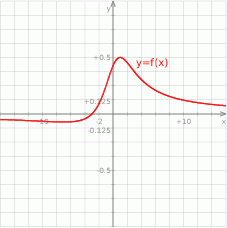
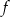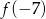Jeżeli teraz naszkicujemy wykres funkcji o takim zachowaniu, to jest jasne, że najmniejsza wartość funkcji f to f(− 7) , a największa to f (1) .

− 4 1 f(− 7) = ----= − --- 56 14 f (1) = 4-= 1. 8 2

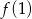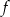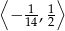
Funkcja f jest funkcją ciągłą na R , więc jej zbiorem wartości jest przedział ⟨ ⟩ − -1, 1 14 2  
Odpowiedź: ⟨ ⟩ − -1, 1 14 2

Wersja PDF