Definicje
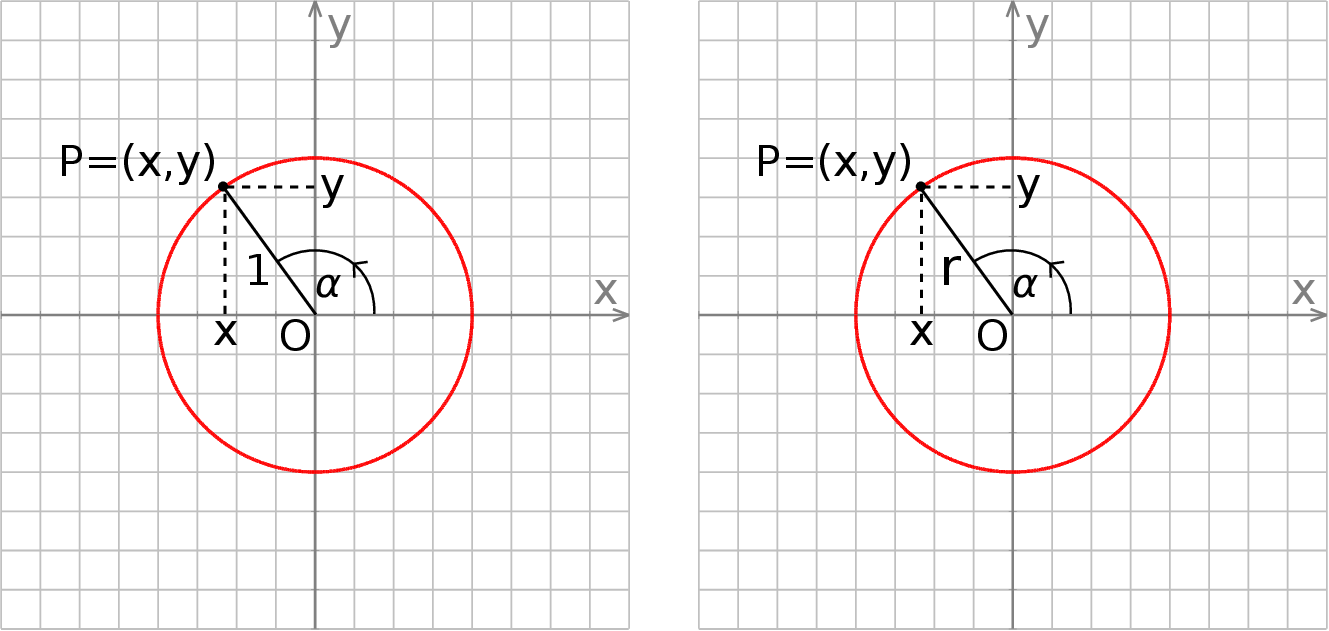
Definicja
Niech 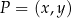 będzie takim punktem na okręgu jednostkowym
będzie takim punktem na okręgu jednostkowym 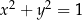 , że półproste
, że półproste 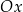 i
i 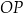 tworzą kąt skierowany o mierze
tworzą kąt skierowany o mierze 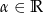 . Definiujemy wtedy
. Definiujemy wtedy

Zdefiniowane wyżej funkcje nazywamy funkcjami trygonometrycznymi.
Fakt 1
Niech 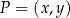 będzie takim punktem na okręgu
będzie takim punktem na okręgu  , że półproste
, że półproste 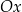 i
i 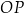 tworzą kąt skierowany o mierze
tworzą kąt skierowany o mierze 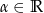 . Wtedy
. Wtedy
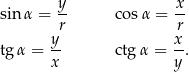
Dowód Okrąg 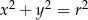 powstaje z okręgu
powstaje z okręgu 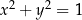 przez jednokładność o środku w punkcie
przez jednokładność o środku w punkcie  i skali
i skali  . Wystarczy teraz zauważyć, że stosunki długości odcinków nie zmieniają się przy jednokładności (bo długość każdego odcinka zmienia się jak mnożenie przez
. Wystarczy teraz zauważyć, że stosunki długości odcinków nie zmieniają się przy jednokładności (bo długość każdego odcinka zmienia się jak mnożenie przez  ).
).
Fakt 2
Jeżeli  jest kątem ostrym w trójkącie prostokątnym, to przy oznaczeniach z rysunku,
jest kątem ostrym w trójkącie prostokątnym, to przy oznaczeniach z rysunku,
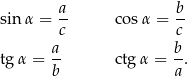

Dowód

Wystarczy w Fakcie 1 oznaczyć 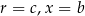 i
i 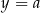 .
.
Proste tożsamości
Twierdzenie3
Dla dowolnego 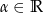 prawdziwa jest równość
prawdziwa jest równość
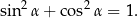
Tożsamość tę nazywamy jedynką trygonometryczną.
Dowód Współrzędne każdego punktu 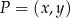 na okręgu jednostkowym spełniają równość (twierdzenie Pitagorasa)
na okręgu jednostkowym spełniają równość (twierdzenie Pitagorasa)
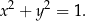
Jeżeli popatrzymy na definicje funkcji sinus i cosinus, to widać, że jest to dokładnie to, co mieliśmy udowodnić.
Fakt 4
Dla dowolnego 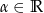 mamy
mamy
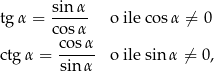
Dowód Bezpośrednio z definicji mamy
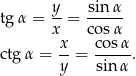
Proste równania i nierówności
Twierdzenie 5
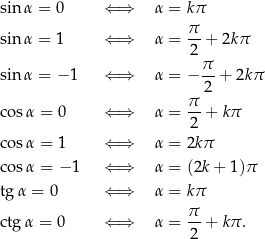
gdzie 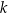 jest dowolną liczba całkowitą.
jest dowolną liczba całkowitą.
Dowód W każdej z równoważności patrzymy na okrąg jednostkowy i sprawdzamy dla jakich kątów  punkt
punkt 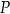 ma odpowiednie współrzędne.
ma odpowiednie współrzędne.
Np. 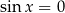 dla punktów, które mają drugą współrzędną zerową, czyli są na osi
dla punktów, które mają drugą współrzędną zerową, czyli są na osi 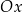 . Punkty te odpowiadają kątom
. Punkty te odpowiadają kątom 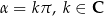 .
.
Podobnie uzasadniamy pozostałe równoważności.
Twierdzenie 6
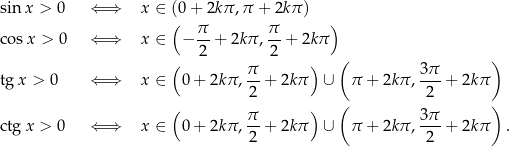
Dowód Jak zwykle patrzymy na obrazek z definicji funkcji trygonometrycznych i sprawdzamy kolejno: kiedy druga współrzędna punktu 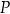 jest dodatnia, kiedy pierwsza współrzędna jest dodatnia, oraz kiedy współrzędne mają ten sam znak.
jest dodatnia, kiedy pierwsza współrzędna jest dodatnia, oraz kiedy współrzędne mają ten sam znak.
Okresowość
Twierdzenie 7
Funkcje sinus i cosinus są okresowe. Okresem podstawowym tych funkcji jest liczba 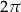 .
.
Dowód To, że liczba 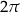 jest okresem jest oczywiste: kąty różniące się o wielokrotność
jest okresem jest oczywiste: kąty różniące się o wielokrotność 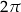 odpowiadają temu samemu punktowi
odpowiadają temu samemu punktowi 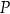 na okręgu jednostkowym.
na okręgu jednostkowym.
Pozostało do wykazania, że jest to okres podstawowy, czyli że żadna mniejsza liczba nie jest okresem tych funkcji.
Przypuśćmy, że 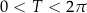 jest okresem funkcji
jest okresem funkcji  , czyli dla dowolnego
, czyli dla dowolnego 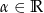 mamy
mamy

Podstawiając w tej równości 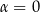 mamy
mamy 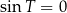 . Na mocy przyjętego założenia
. Na mocy przyjętego założenia 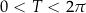 i Twierdzenia 5, mamy zatem
i Twierdzenia 5, mamy zatem 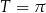 . To jednak nie jest możliwe, bo
. To jednak nie jest możliwe, bo
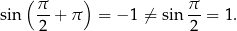
Podobnie postępujemy w przypadku funkcji cosinus. W równości
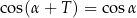
podstawiamy 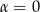 , co daje nam
, co daje nam 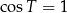 . Jest sprzeczne z Twierdzeniem 5 (bo
. Jest sprzeczne z Twierdzeniem 5 (bo 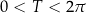 ).
).
Twierdzenie 8
Funkcje tangens i cotangens są okresowe. Okresem podstawowym tych funkcji jest liczba 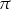 .
.
Dowód Jest jasne, że liczba 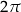 jest okresem. To, że liczba
jest okresem. To, że liczba 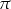 też jest okresem można zobaczyć następująco. Patrzymy na obrazek z definicji funkcji trygonometrycznych.
też jest okresem można zobaczyć następująco. Patrzymy na obrazek z definicji funkcji trygonometrycznych.
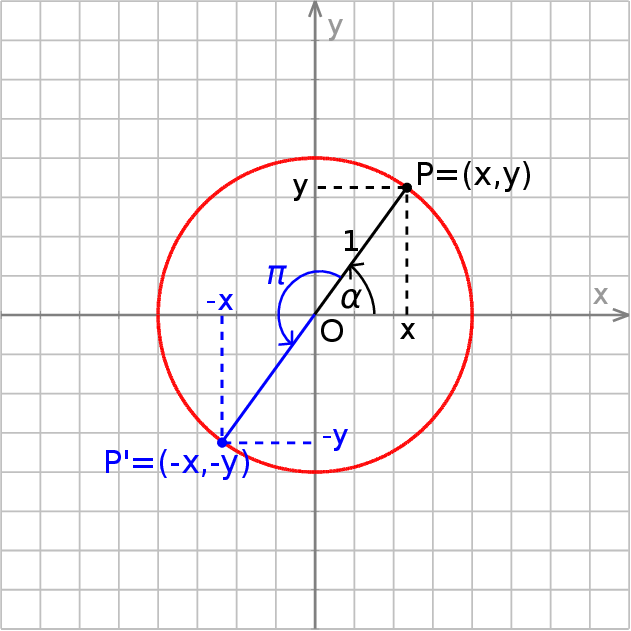
Dodanie kąta  do kąta
do kąta  odpowiada obróceniu półprostej
odpowiada obróceniu półprostej  o
o 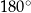 . Można też myśleć, że jest to odbicie punktu
. Można też myśleć, że jest to odbicie punktu 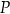 względem środka
względem środka 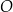 początku układu współrzędnych. W wyniku takiej operacji współrzędne punktu
początku układu współrzędnych. W wyniku takiej operacji współrzędne punktu  zmienią znak na przeciwny. To jednak oznacza, że funkcje tangens i cotangens nie zmienią wartości.
zmienią znak na przeciwny. To jednak oznacza, że funkcje tangens i cotangens nie zmienią wartości.
Pozostało do wykazania, że jest to okres podstawowy. Załóżmy, że 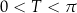 jest okresem funkcji tangens, czyli dla dowolnego
jest okresem funkcji tangens, czyli dla dowolnego 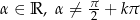 mamy
mamy
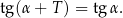
Wstawiając 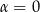 mamy
mamy 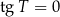 . To jednak jest niemożliwe na mocy naszego założenia
. To jednak jest niemożliwe na mocy naszego założenia 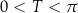 i Twierdzenia 5.
i Twierdzenia 5.
Podobnie uzasadniamy, że liczba 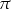 jest okresem podstawowym funkcji cotangens.
jest okresem podstawowym funkcji cotangens.
Twierdzenie 9
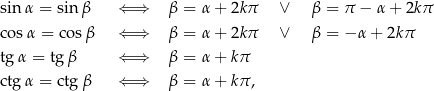
gdzie 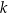 oznacza dowolną liczbę całkowita.
oznacza dowolną liczbę całkowita.
Dowód Jeżeli 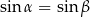 , to odpowiadające tym kątom punkty na okręgu jednostkowym mają taką samą drugą współrzędną. Jeżeli te punkty się pokrywają, to mamy
, to odpowiadające tym kątom punkty na okręgu jednostkowym mają taką samą drugą współrzędną. Jeżeli te punkty się pokrywają, to mamy  . Jeżeli natomiast są dwa różne punkty, to muszą leżeć symetrycznie względem osi
. Jeżeli natomiast są dwa różne punkty, to muszą leżeć symetrycznie względem osi  . To jednak oznacza, że
. To jednak oznacza, że 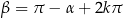 .
.
Podobnie uzasadniamy drugą równoważność.
Patrząc na definicje funkcji trygonometrycznych łatwo zauważyć, że tangens jest rosnący w przedziałach 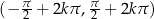 i
i  . Zatem na okręgu jednostkowym są co najwyżej dwa punkty, dla których tangensy odpowiadających kątów są równe
. Zatem na okręgu jednostkowym są co najwyżej dwa punkty, dla których tangensy odpowiadających kątów są równe 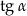 . Z drugiej strony, z okresowości tangensa wiemy, że
. Z drugiej strony, z okresowości tangensa wiemy, że  . Zatem równość
. Zatem równość 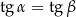 oznacza, że
oznacza, że 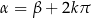 (jeżeli odpowiadające punkty się pokrywają) lub
(jeżeli odpowiadające punkty się pokrywają) lub 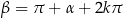 (jeżeli punkty są różne). Oba warunki można krótko zapisać w postaci
(jeżeli punkty są różne). Oba warunki można krótko zapisać w postaci 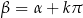 .
.
Podobnie rozumujemy w przypadku cotangensa (lub korzystamy ze wzoru 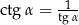 ).
).
Wzory redukcyjne
Twierdzenie 10
Niech zapis 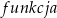 oznacza jedną funkcji trygonometrycznych, a zapis
oznacza jedną funkcji trygonometrycznych, a zapis 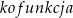 , niech będzie odpowiadającą kofunkcją do
, niech będzie odpowiadającą kofunkcją do 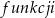 , według schematu
, według schematu

Wtedy dla dowolnego 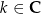 mamy zależność
mamy zależność
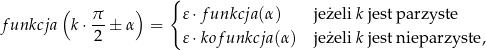
gdzie  jest znakiem wyrażenia
jest znakiem wyrażenia 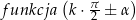 po podstawieniu za
po podstawieniu za  dowolnego kąta ostrego.
dowolnego kąta ostrego.
Dowód Patrząc ponownie na koło jednostkowe, łatwo zauważyć, że następujące operacje: dodanie lub odjęcie kąta 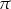 do
do  , zamiana
, zamiana  na
na  , nie zmieniają wartości bezwzględnych współrzędnych punktu
, nie zmieniają wartości bezwzględnych współrzędnych punktu 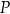 (czyli co najwyżej zmieniają znaki współrzędnych tego punktu).
(czyli co najwyżej zmieniają znaki współrzędnych tego punktu).
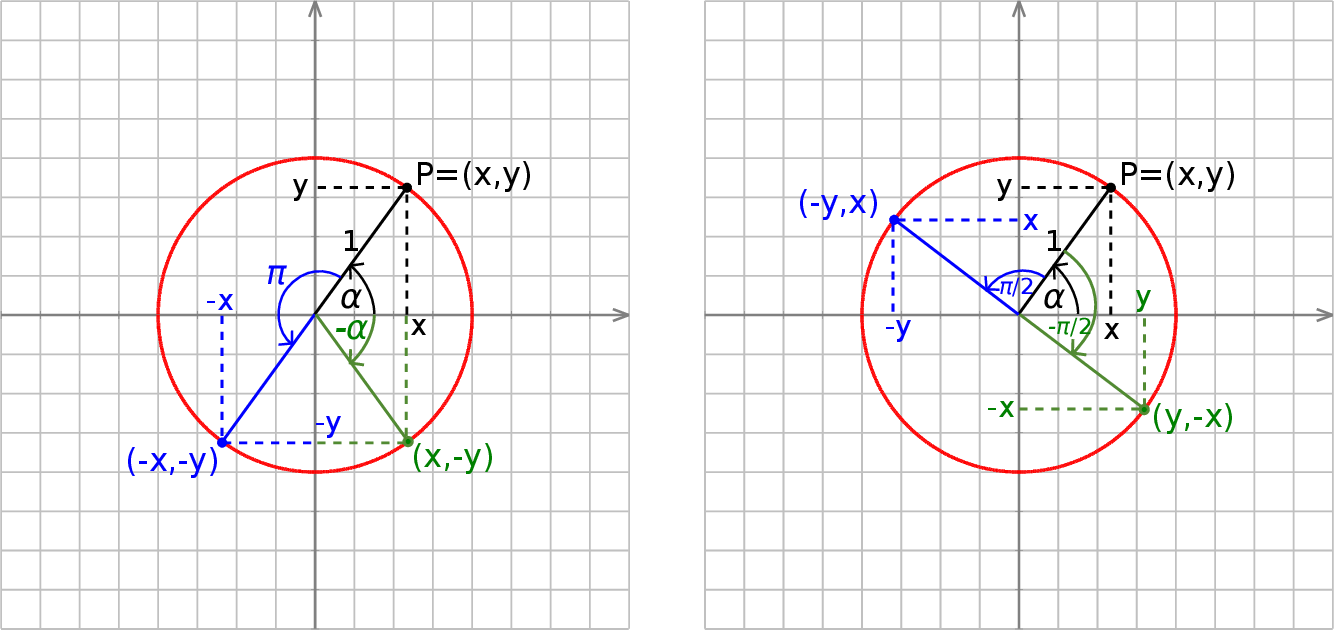
To oznacza, że dodawanie/odejmowanie dowolnej wielokrotności kąta  do argumentu którejkolwiek funkcji trygonometrycznej nie zmienia wartości bezwzględnej tej funkcji (czyli co najwyżej zmienia jej znak). Podobnie w przypadku zamiany kąta na kąt przeciwny. W szczególności uzasadniliśmy równość
do argumentu którejkolwiek funkcji trygonometrycznej nie zmienia wartości bezwzględnej tej funkcji (czyli co najwyżej zmienia jej znak). Podobnie w przypadku zamiany kąta na kąt przeciwny. W szczególności uzasadniliśmy równość

Podobnie, łatwo sprawdzić na okręgu jednostkowym, że dodatnie/odjęcie do kąta  kąta
kąta  , powoduje zamianę wartości bezwzględnych współrzędnych punktu
, powoduje zamianę wartości bezwzględnych współrzędnych punktu  (czyli współrzędne te zamieniają się miejscami i ewentualnie zmieniają znaki). W połączeniu z uzasadnioną już niezmienniczością na dodawanie/odejmowanie wielokrotności kąta
(czyli współrzędne te zamieniają się miejscami i ewentualnie zmieniają znaki). W połączeniu z uzasadnioną już niezmienniczością na dodawanie/odejmowanie wielokrotności kąta 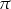 , oraz na zmianę kąta na przeciwny, daje nam to
, oraz na zmianę kąta na przeciwny, daje nam to
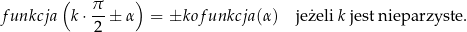
Pozostało ustalić jaki powinien być znak z prawej strony tych wzorów. Aby to zrobić, wystarczy sprawdzić jakie są znaki obu stron dla jednego dowolnie wybranego kąta. Jeżeli wybierzemy kąt ostry  , to zarówno
, to zarówno 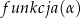 jak i
jak i 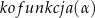 są dodatnie i za
są dodatnie i za  trzeba wziąć znak wyrażenia
trzeba wziąć znak wyrażenia 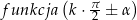
Funkcje sumy i różnicy kątów
Twierdzenie 11
Dla dowolnych 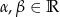 prawdziwe są wzory
prawdziwe są wzory
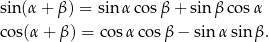
Dowód W dowodzie użyjemy rachunku wektorowego. Zacznijmy od narysowania w układzie współrzędnych wektora jednostkowego 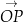 o początku w punkcie
o początku w punkcie  i tworzącego z osią
i tworzącego z osią  kąt
kąt  .
.
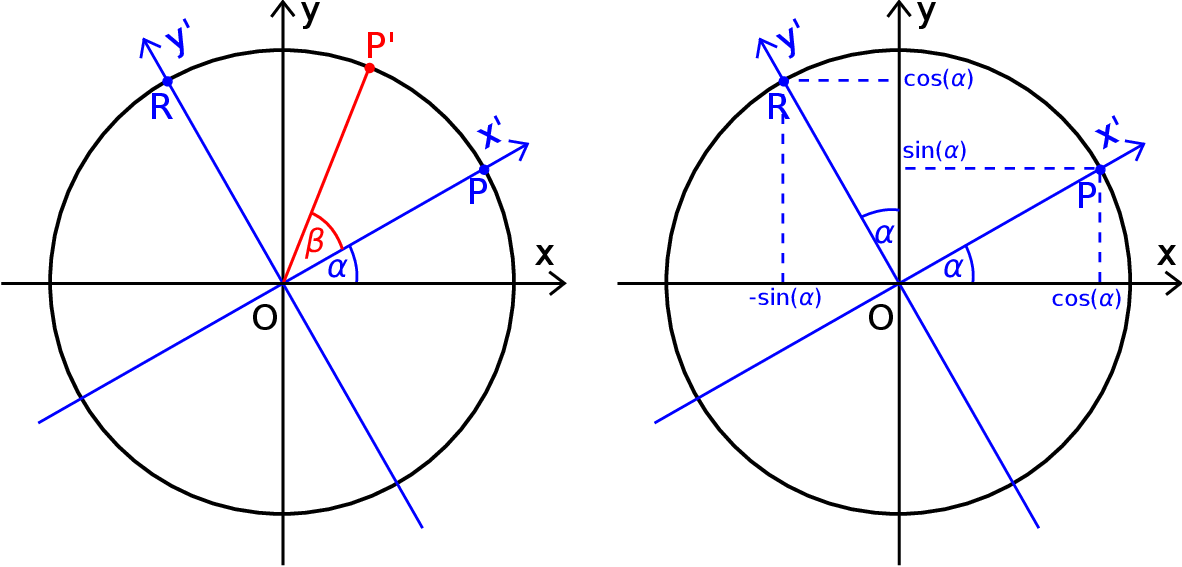
Wtedy 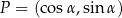 . Niech
. Niech 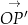 będzie wektorem, który powstaje z
będzie wektorem, który powstaje z  przez obrót względem punktu
przez obrót względem punktu 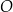 o kąt
o kąt  . Oczywiście
. Oczywiście
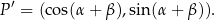
Spróbujemy teraz wyliczyć współrzędne punktu 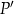 w inny sposób.
w inny sposób.
Niech 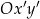 będzie układem współrzędnych, który powstaje z
będzie układem współrzędnych, który powstaje z 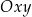 przez obrót względem punktu
przez obrót względem punktu 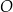 o kąt
o kąt  . W szczególności oś
. W szczególności oś 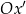 jest wyznaczona przez wektor
jest wyznaczona przez wektor ![→ OP = [cosα,sin α]](https://img.zadania.info/por/0024654/HporT136x.png) . W takim razie druga oś jest wyznaczona przez wektor
. W takim razie druga oś jest wyznaczona przez wektor 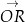 , który jest prostopadły do
, który jest prostopadły do 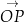 . Łatwo odgadnąć współrzędne tego wektora:
. Łatwo odgadnąć współrzędne tego wektora: ![→ OR = [− sin α,co sα]](https://img.zadania.info/por/0024654/HporT139x.png) (prawy obrazek).
(prawy obrazek).
W układzie współrzędnych 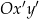 wektor
wektor 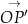 ma współrzędne
ma współrzędne ![[cos β,sinβ ]](https://img.zadania.info/por/0024654/HporT142x.png) (bo tworzy kąt
(bo tworzy kąt 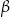 z osią
z osią 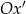 ), co nam daje następujące współrzędne w układzie
), co nam daje następujące współrzędne w układzie  .
.
![→ → → OP ′ = cos β⋅OP + sin β ⋅OR = co sβ ⋅[cosα ,sin α]+ sin β ⋅[− sinα ,cosα] = = [cosβ cos α− sin β sin α,co sβ sin α + sinβ cos α].](https://img.zadania.info/por/0024654/HporT146x.png)
W połączeniu z wcześniej zauważoną równością
![→ ′ OP = [cos(α+ β),sin(α + β)]](https://img.zadania.info/por/0024654/HporT147x.png)
daje to nam żądane równości.
Twierdzenie 12
Dla dowolnych 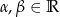 prawdziwe są wzory
prawdziwe są wzory
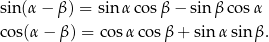
Dowód Podstawiamy we wzorach z poprzedniego twierdzenia 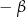 zamiast
zamiast 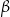 .
.
Twierdzenie 13
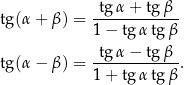
Dowód Liczymy (korzystając z Twierdzenia 11)
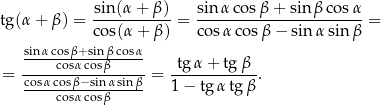
Drugi wzór otrzymujemy z pierwszego podstawiając  zamiast
zamiast 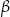 .
.
Funkcje podwojonego kąta
Twierdzenie 14

Dowód Pierwsze dwa wzory otrzymujemy podstawiając 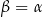 w Twierdzeniu 11 oraz korzystając z jedynki trygonometrycznej. Trzeci wzór otrzymujemy biorąc
w Twierdzeniu 11 oraz korzystając z jedynki trygonometrycznej. Trzeci wzór otrzymujemy biorąc 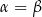 w Twierdzeniu 13.
w Twierdzeniu 13.
Twierdzenie 15
Jeżeli oznaczymy 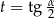 to
to
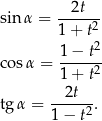
Dowód Liczymy (korzystamy z Twierdzenia 14)
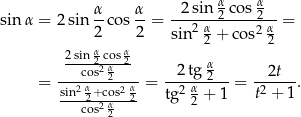
Podobnie liczymy dla cosinusa.
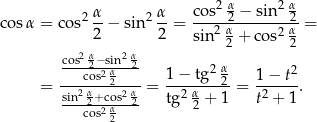
Jeszcze wzór dla tangensa.

Sumy i różnice funkcji
Twierdzenie 16
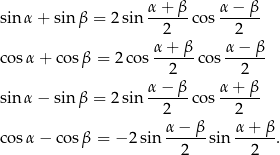
Dowód Jeżeli w pierwszym wzorze podstawimy 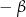 zamiast
zamiast 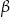 , otrzymamy trzeci wzór. Podobnie, podstawiając
, otrzymamy trzeci wzór. Podobnie, podstawiając 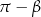 w drugim wzorze, otrzymamy czwarty wzór. Wystarczy zatem udowodnić dwa pierwsze wzory.
w drugim wzorze, otrzymamy czwarty wzór. Wystarczy zatem udowodnić dwa pierwsze wzory.
Liczymy (korzystamy z Twierdzeń 11 i 12)
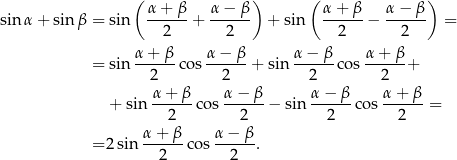
Podobnie jest z drugą równością
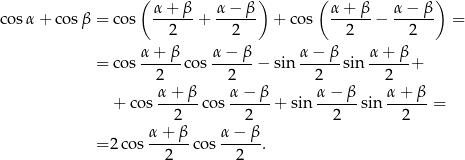
Wartości funkcji trygonometrycznych dla wybranych kątów.
Twierdzenie 17
| kąt | 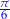 | 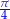 | 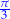 |
| sinus |  | 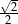 | 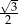 |
| cosinus | 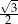 |  | 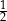 |
Dowód Zacznijmy od kąta 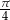 . Rysujemy połówkę kwadratu o boku 1.
. Rysujemy połówkę kwadratu o boku 1.

Przekątna tego kwadratu ma długość 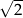 , więc
, więc
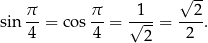
Aby uzasadnić pozostałe równości rysujemy trójkąt równoboczny o boku 1. Z twierdzenia Pitagorasa łatwo wyliczyć, że wysokość tego trójkąta jest równa 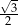 . Daje to nam
. Daje to nam

Twierdzenie 18

Dowód Korzystamy ze wzorów na  i
i 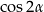 (Twierdzenie 14) oraz ze wzoru
(Twierdzenie 14) oraz ze wzoru  .
.
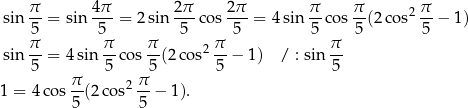
Podstawiamy teraz 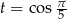 .
.
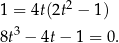
Łatwo znaleźć pierwiastek 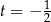 tego równania. Dzielmy więc przez
tego równania. Dzielmy więc przez 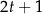 .
.
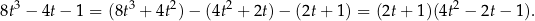
Wiemy, że 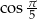 jest dodatni, więc jest to dodatni pierwiastek równania kwadratowego w nawiasie
jest dodatni, więc jest to dodatni pierwiastek równania kwadratowego w nawiasie
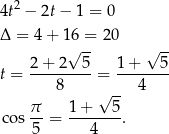
Z jedynki trygonometrycznej wyliczamy
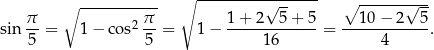
Tips & Tricks
1Definicja funkcji trygonometrycznych przy pomocy okręgu jednostkowego jest bardzo wygodna, bo pozwala zdefiniować te funkcje dla dowolnej wartości kąta. Jest ona również historycznie wcześniejsza od definicji używającej trójkąta prostokątnego.
Z drugiej strony, definicja funkcji w trójkącie prostokątnym (Fakt 2) jest o wiele prostsza i lepiej oddaje geometryczny charakter funkcji trygonometrycznych.
2Zaznaczając kąty w układzie współrzędnych zwykle rysowaliśmy ostry kąt  . Warto jednak zadać sobie trud i posprawdzać, że rysując kąty w innych ćwiartkach nasze argumenty pozostają bez zmian.
. Warto jednak zadać sobie trud i posprawdzać, że rysując kąty w innych ćwiartkach nasze argumenty pozostają bez zmian.
3Jedynka trygonometryczna (Twierdzenie 3) jest dokładnie zapisem twierdzenia Pitagorasa – szczególnie dobrze to widać patrząc na definicje sinusa i cosinusa w trójkącie prostokątnym.
4Twierdzenie 6 jest zwykle uczone w postaci formułki w pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus.
5Twierdzenie 7 na ogół pojawia się w podręcznikach w postaci liczba 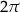 jest okresem funkcji.... My wykazujemy jednak znacznie więcej: pokazujemy, że żadna mniejsza liczba nie jest okresem tych funkcji. Podobnie w przypadku Twierdzenia 8.
jest okresem funkcji.... My wykazujemy jednak znacznie więcej: pokazujemy, że żadna mniejsza liczba nie jest okresem tych funkcji. Podobnie w przypadku Twierdzenia 8.
6Nasz dowód Twierdzenia 9 nie jest w pełni precyzyjny, ale za to bardzo geometryczny. Precyzyjny dowód można przeprowadzić używając wzorów na różnice funkcji trygonometrycznych (Twierdzenie 16).
7Twierdzenie 10 zawiera najogólniejszą postać wzorów redukcyjnych i pomimo swojego pozornego skomplikowania, jest to najlepszy sposób na zapamiętanie wszystkich wzór redukcyjnych na raz.
Wzór ten jest formalnym zapisaniem tego, że obracając się na okręgu co 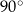 zamieniamy współrzędne punktu ze sobą i zmieniamy znak jednej z nich. Gdy się to dokładnie napisze wyjdzie Twierdzenie 10.
zamieniamy współrzędne punktu ze sobą i zmieniamy znak jednej z nich. Gdy się to dokładnie napisze wyjdzie Twierdzenie 10.
8Twierdzenie 11 jest zdecydowanie najważniejszym twierdzeniem trygonometrii. Wszystkie tożsamości trygonometryczne są jego konsekwencjami: jedynkę otrzymujemy biorąc  w wzorze na
w wzorze na 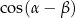 , każdy wzór redukcyjny jest tej postaci, wzory na sumy i różnice funkcji są konsekwencjami tych wzorów – Twierdzenie 16.
, każdy wzór redukcyjny jest tej postaci, wzory na sumy i różnice funkcji są konsekwencjami tych wzorów – Twierdzenie 16.
9Przedstawiony dowód Twierdzenia 11 jest bardzo elegancki z kilku powodów. Przed wszystkim, nie trzeba w nim nic zakładać o kątach  i
i 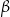 – w większości innych dowodów tego twierdzenia, dowodzi się tych wzorów przy założeniu
– w większości innych dowodów tego twierdzenia, dowodzi się tych wzorów przy założeniu  , a potem przechodzi się do sytuacji ogólnej ze wzorów redukcyjnych. Przy naszym podejściu, wzory redukcyjne możemy traktować jako wniosek z Twierdzenia 11.
, a potem przechodzi się do sytuacji ogólnej ze wzorów redukcyjnych. Przy naszym podejściu, wzory redukcyjne możemy traktować jako wniosek z Twierdzenia 11.
Kolejną zaletą tego dowodu jest to, że otrzymujemy oba wzory (na sinus sumy i cosinus sumy) jednocześnie. Wbrew pozorom, otrzymanie z jednego wzoru z drugiego jest dość podchwytliwe. Jeżeli np. umiemy udowodnić wzór na sinus sumy dla kątów ostrych, to nie ma prostego sposobu na wyprowadzenie stąd wzoru na cosinus sumy. Sztuczki w stylu zamiana  na
na 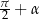 wymagają znajomości wzoru na sinus sumy dla kątów większych od
wymagają znajomości wzoru na sinus sumy dla kątów większych od 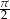 , a tego większość innych dowodów nie daje.
, a tego większość innych dowodów nie daje.
10 O dowodzie Twierdzenia 11 należy myśleć następująco. Uzasadniliśmy, że pomiędzy współrzędnymi 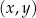 w układzie
w układzie 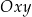 , a współrzędnymi
, a współrzędnymi 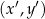 w układzie
w układzie 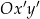 zachodzi związek
zachodzi związek
![→ → [x,y] = x′ ⋅OP + y′ ⋅OR = [x ′cosα − y′sin α,x′sin α+ y′cosα ].](https://img.zadania.info/por/0024654/HporT213x.png)
O wzorze tym należy myśleć jak o wzorze na współrzędne punktu 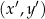 po obrocie o kąt
po obrocie o kąt  . Jeżeli teraz do tego wzoru wstawimy punkt
. Jeżeli teraz do tego wzoru wstawimy punkt 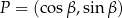 to trzymamy współrzędne punktu
to trzymamy współrzędne punktu 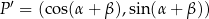 .
.
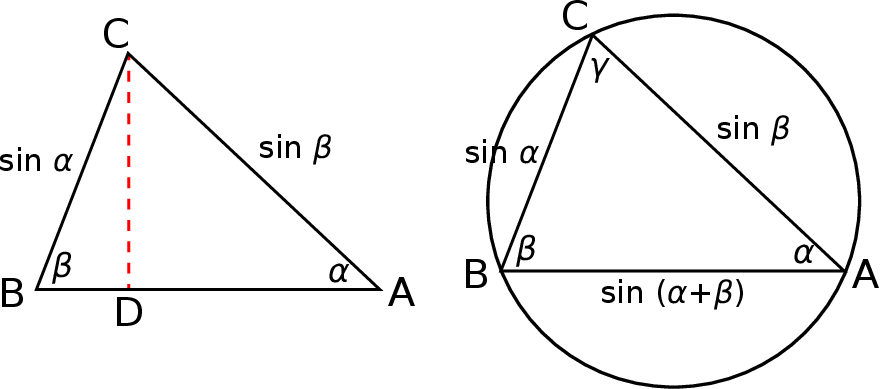
11Wzory z Twierdzenia 11 mają bardzo prostą interpretację geometryczną w języku twierdzenia sinusów. Zajmiemy się tylko pierwszym wzorem.
Jeżeli trójkąt o kątach  i
i 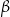 jest wpisany w okrąg o średnicy 1, to z twierdzenia sinusów łatwo zauważyć, że jego boki mają długości
jest wpisany w okrąg o średnicy 1, to z twierdzenia sinusów łatwo zauważyć, że jego boki mają długości 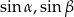 i
i 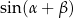 .
.
Wtedy wzór na sinus sumy sprowadza się do równości 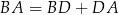 , gdzie
, gdzie 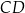 jest wysokością opuszczoną na bok
jest wysokością opuszczoną na bok 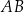 .
.
Po interpretację drugiego wzoru, jak i po inne dowody Twierdzenia 11 odsyłam czytelnika do www.zadania.info/6783108.
12Twierdzenie 15 ma duże znaczenie teoretyczne, bo pokazuje, że wykonując podstawienie z jego treści, można dowolne wyrażenie z funkcjami trygonometrycznymi zamienić na wyrażenie bez funkcji trygonometrycznych (o ile wszystkie funkcje mają tren sam argument!). W praktyce jest to nagminnie stosowane w rachunku całkowym.
13Twierdzenie 18 jest blisko związane z geometrią pięciokąta foremnego i ma prosty dowód geometryczny – www.zadania.info/3024938
14W Twierdzeniach 17 i 18 wypisaliśmy tylko wartości funkcji sinus i cosinus, ale wyliczenie z nich wartości funkcji tangens i cotangens jest już natychmiastowe.
15Wyznaczone wzory na funkcje trygonometryczne kątów 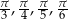 są blisko związane z faktem, że trójkąt równoboczny, kwadrat, pięciokąt i sześciokąt foremny można skonstruować przy pomocy cyrkla i linijki. Tymczasem można udowodnić, że nie da się skonstruować siedmiokąta foremnego, co wiąże się tym, że nie ma wzorków na funkcje kąta
są blisko związane z faktem, że trójkąt równoboczny, kwadrat, pięciokąt i sześciokąt foremny można skonstruować przy pomocy cyrkla i linijki. Tymczasem można udowodnić, że nie da się skonstruować siedmiokąta foremnego, co wiąże się tym, że nie ma wzorków na funkcje kąta  .
.
Co ciekawe, można skonstruować 17-kąt foremny, co oznacza, że są wzorki na  i
i 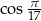 . Wzory te jednak są dość skomplikowane:
. Wzory te jednak są dość skomplikowane:
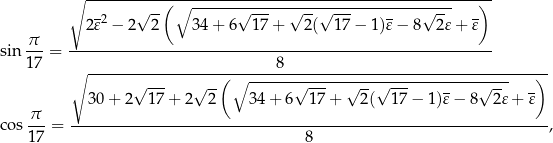
gdzie 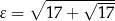 i
i 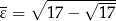 .
.
Wzorki te znał już Gauss pod koniec XVIII wieku.

