/Szkoła średnia/Funkcje

Zadanie nr 2612327

Dodaj do ulubionych
Dodaj do rozwiązanych

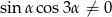Wykaż, że dla dowolnego kąta α takiego, że sin α cos3 α ⁄= 0 zachodzi tożsamość

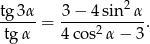
2 tg3α-= 3-−-4-sin--α-. tg α 4 cos2α − 3

Rozwiązanie

Będziemy korzystać ze wzorów

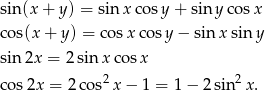
sin(x + y) = sin xc osy + siny cos x cos(x + y ) = cosx cos y− sin x sin y sin2x = 2 sin x cosx cos 2x = 2 cos2x − 1 = 1− 2sin2 x.

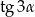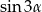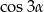Po lewej stronie występuje tg 3α , wyliczymy go licząc sin 3α i co s3α . Najpierw liczymy 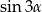sin 3α – będziemy starać się otrzymać wyrażenie bez cosα .

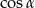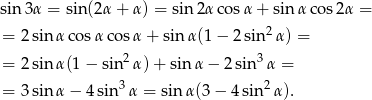
sin 3α = sin (2α+ α) = sin 2αco sα + sinα cos 2α = = 2sinα cos αco sα + sinα (1− 2 sin2α ) = 2 3 = 2sinα (1− sin α) + sinα − 2 sin α = = 3sinα − 4 sin3α = sin α(3 − 4 sin 2α).

Podobnie obliczamy 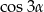co s3α – staramy się nie mieć sin α .

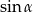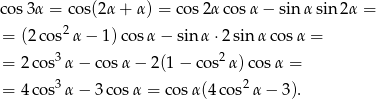
co s3α = cos(2α + α) = c os2α cos α− sin α sin 2α = 2 = (2 cos α − 1 )cos α− sin α ⋅2sin αco sα = = 2 cos3α − co sα − 2(1 − cos2 α)co sα = = 4 cos3α − 3 cos α = cos α(4co s2α − 3).

Stąd

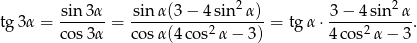
2 2 tg 3α = sin-3α--= -sin-α(3-−-4-sin--α)-= tgα ⋅-3−-4-sin-α-. cos3α co sα(4 cos2α − 3) 4 cos2α − 3

Po podzieleniu tej równości stronami przez 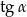tg α otrzymujemy tożsamość, którą mieliśmy udowodnić.

Wersja PDF