O funkcji liczbowej myślimy jak o maszynce, która po otrzymaniu jednej liczby (argumentu) zwraca nam inną liczbę (wartość). Jednym ze sposobów reprezentowania funkcji jest wykres. Wykres tworzymy zaznaczając w układzie współrzędnych wszystkie punkty postaci 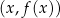 , gdzie parametr
, gdzie parametr  przebiega całą dziedzinę funkcji. Na ogół dziedzina funkcji jest zbiorem nieskończonym (np. całym zbiorem
przebiega całą dziedzinę funkcji. Na ogół dziedzina funkcji jest zbiorem nieskończonym (np. całym zbiorem 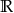 liczb rzeczywistych), więc gdy zaznaczymy wszystkie punkty wykresu, otrzymamy pewną krzywą.
liczb rzeczywistych), więc gdy zaznaczymy wszystkie punkty wykresu, otrzymamy pewną krzywą.
Wykres funkcji 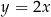 składa się ze wszystkich punktów postaci
składa się ze wszystkich punktów postaci 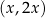 , gdzie
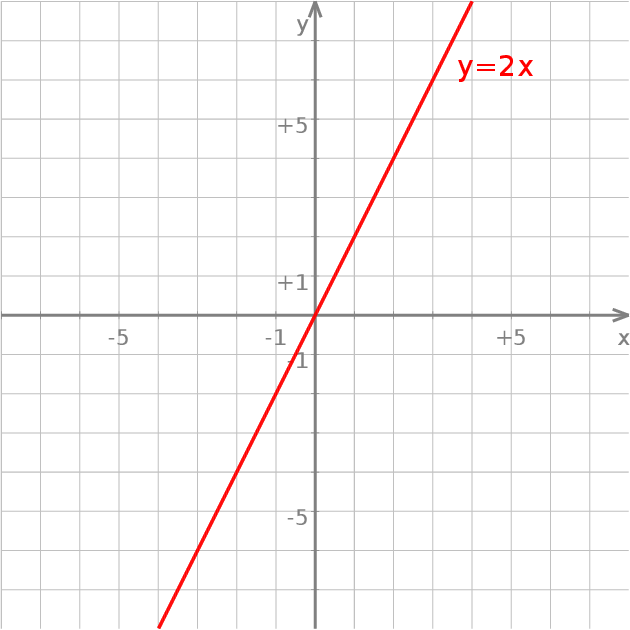
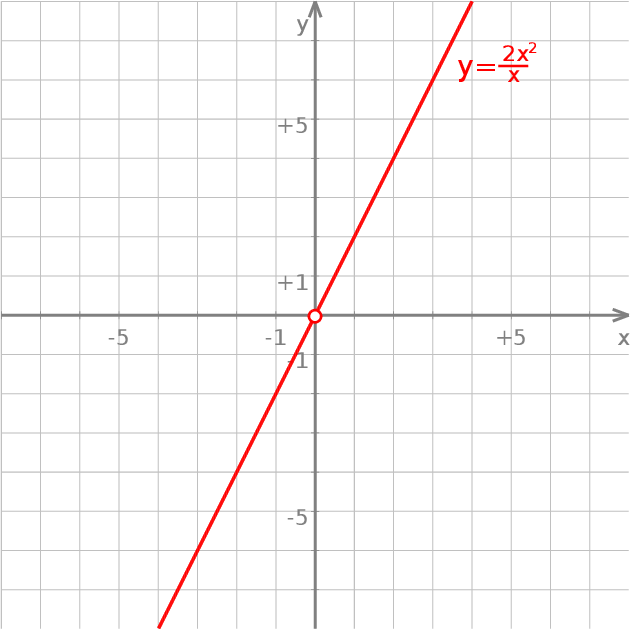
, gdzie 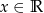 , czyli z punktów, których druga współrzędna jest dwa razy większa od pierwszej. Jak dobrze wiemy, wszystkie te punkty leżą na jednej prostej.
, czyli z punktów, których druga współrzędna jest dwa razy większa od pierwszej. Jak dobrze wiemy, wszystkie te punkty leżą na jednej prostej.
Jeżeli chcemy zaznaczyć, że pewien punkt nie należy do wykresu funkcji to zaznaczamy to rysując w jego miejscu małe puste kółeczko. Pełne kółko (kropka) oznacza punkt, który do wykresu należy.
Funkcja 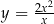 jest oczywiście równa funkcji
jest oczywiście równa funkcji 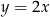 . Jednak ze względu na
. Jednak ze względu na  w mianowniku, do jej dziedziny nie należy 0. Na wykresie zaznaczamy to usuwając punkt o pierwszej współrzędnej równej 0.
w mianowniku, do jej dziedziny nie należy 0. Na wykresie zaznaczamy to usuwając punkt o pierwszej współrzędnej równej 0.
Na obrazku naszkicowaliśmy wykres funkcji signum (znak)
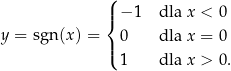

Odczytywanie własności funkcji z wykresu Mając dany wykres funkcji, jesteśmy w stanie odczytać niektóre jej własności (pomimo, że nie mamy wzoru funkcji).
Dziedziną funkcji jest zbiór wszystkich liczb na osi 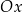 , nad którymi jest jakiś punkt wykresu. Wygodny sposób ustalenia dziedziny to wyobrażenie sobie, że rzutujemy cały wykres funkcji na oś
, nad którymi jest jakiś punkt wykresu. Wygodny sposób ustalenia dziedziny to wyobrażenie sobie, że rzutujemy cały wykres funkcji na oś 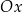 (czyli przesuwamy każdy punkt wykresu pionowo, aż znajdzie się na osi
(czyli przesuwamy każdy punkt wykresu pionowo, aż znajdzie się na osi 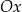 ). Zbiór, który otrzymamy na osi
). Zbiór, który otrzymamy na osi 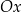 to dokładnie dziedzina funkcji.
to dokładnie dziedzina funkcji.
Dziedziną funkcji na lewym wykresie jest zbiór 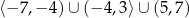 (zaznaczyliśmy ten zbiór na niebiesko).
(zaznaczyliśmy ten zbiór na niebiesko).
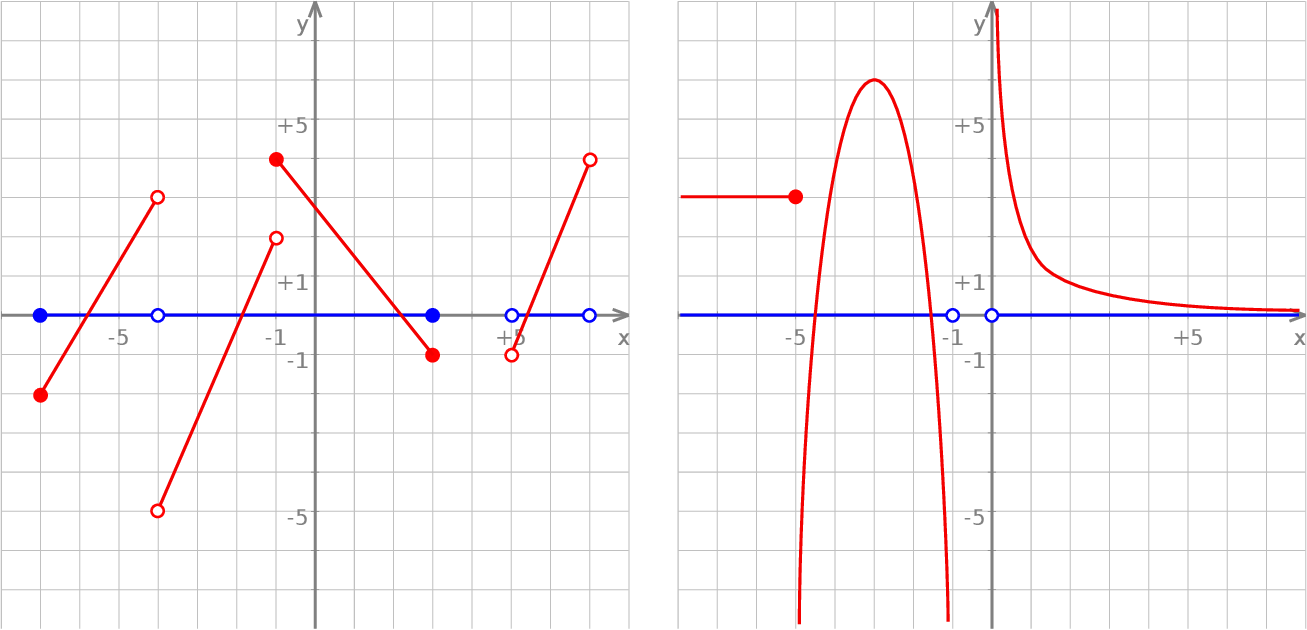
Dziedziną funkcji z prawego wykresu jest zbiór 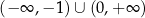 .
.
Zbiorem wartości funkcji jest zbiór wszystkich liczb na osi 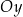 , na których poziomie jest jakiś punkt wykresu. Wygodny sposób ustalenia dziedziny to wyobrażenie sobie, że rzutujemy cały wykres funkcji na oś
, na których poziomie jest jakiś punkt wykresu. Wygodny sposób ustalenia dziedziny to wyobrażenie sobie, że rzutujemy cały wykres funkcji na oś 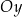 (czyli przesuwamy każdy punkt wykresu poziomo, aż znajdzie się na osi
(czyli przesuwamy każdy punkt wykresu poziomo, aż znajdzie się na osi 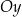 ). Zbiór, który otrzymamy na osi
). Zbiór, który otrzymamy na osi  to dokładnie zbiór wartości funkcji.
to dokładnie zbiór wartości funkcji.
Czasami dodatkowo musimy podać najmniejszą bądź największą wartość funkcji: są to po prostu lewy i prawy koniec zbioru wartości (jeżeli istnieją!).
Zbiorem wartości funkcji na lewym wykresie jest zbiór 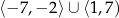 (zaznaczyliśmy ten zbiór na niebiesko). Wartością najmniejszą tej funkcji jest
(zaznaczyliśmy ten zbiór na niebiesko). Wartością najmniejszą tej funkcji jest 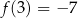 , a wartość największa nie istnieje (bo funkcja przyjmuje wartości dowolnie bliskie 7, ale nie przyjmuje wartości 7).
, a wartość największa nie istnieje (bo funkcja przyjmuje wartości dowolnie bliskie 7, ale nie przyjmuje wartości 7).
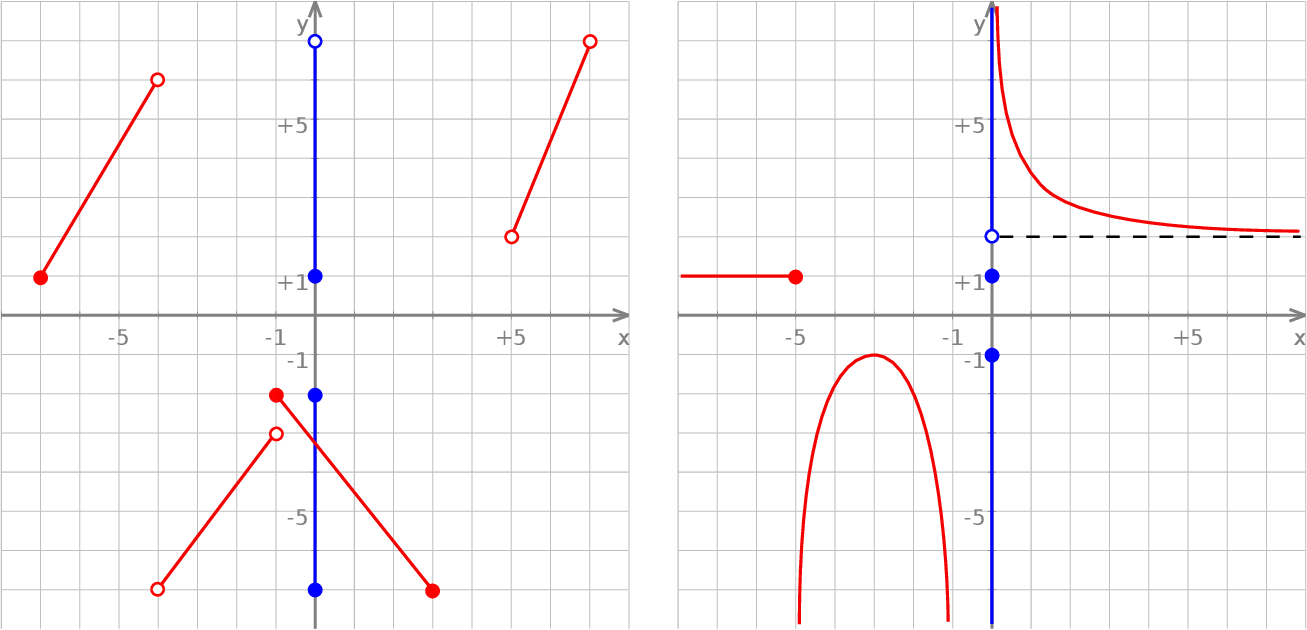
Zbiorem wartości funkcji z prawego wykresu jest zbiór 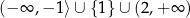 .
.
Rozwiązania równania 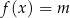 znajdujemy szukając punktów wspólnych danego wykresu oraz poziomej prostej
znajdujemy szukając punktów wspólnych danego wykresu oraz poziomej prostej 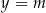 . Miejsca zerowe otrzymujemy dla
. Miejsca zerowe otrzymujemy dla 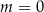 , czyli szukając punktów wspólnych danego wykresu i osi
, czyli szukając punktów wspólnych danego wykresu i osi 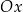 .
.
Z podanego wykresu funkcji 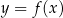 odczytajmy rozwiązania równania
odczytajmy rozwiązania równania 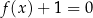 , oraz rozwiązanie nierówności
, oraz rozwiązanie nierówności 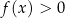 .
.
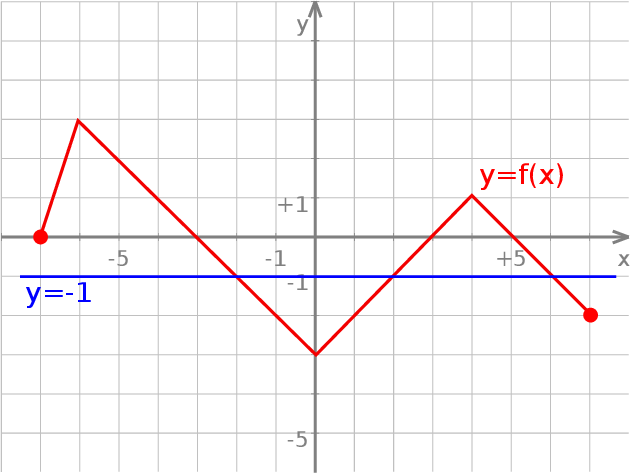
Równanie 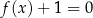 jest równoważne równaniu
jest równoważne równaniu 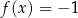 , czyli szukamy punktów wspólnych danego wykresu i prostej
, czyli szukamy punktów wspólnych danego wykresu i prostej 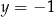 . Rozwiązaniami są
. Rozwiązaniami są 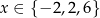 .
.
Podobnie odczytujemy rozwiązanie nierówności 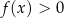 : patrzymy dla jakich argumentów wykres funkcji jest powyżej osi
: patrzymy dla jakich argumentów wykres funkcji jest powyżej osi 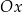 . Odpowiedzią jest zbiór
. Odpowiedzią jest zbiór 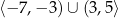 .
.
Przedziały monotoniczności odczytujemy patrząc, na jakich przedziałach funkcja rośnie, a na jakich maleje. Przypomnijmy, że funkcja rośnie, gdy jej wykres „jedzie do góry” jeżeli przesuwamy się po nim w kierunku strzałki na osi 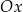 (czyli w prawo). Podobnie, funkcja maleje, gdy jej wykres „jedzie w dół”.
(czyli w prawo). Podobnie, funkcja maleje, gdy jej wykres „jedzie w dół”.
Funkcja przedstawiona na lewym wykresie rośnie na przedziałach 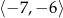 oraz
oraz 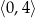 . Ta sama funkcja maleje na przedziałach
. Ta sama funkcja maleje na przedziałach 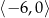 i
i 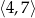 .
.
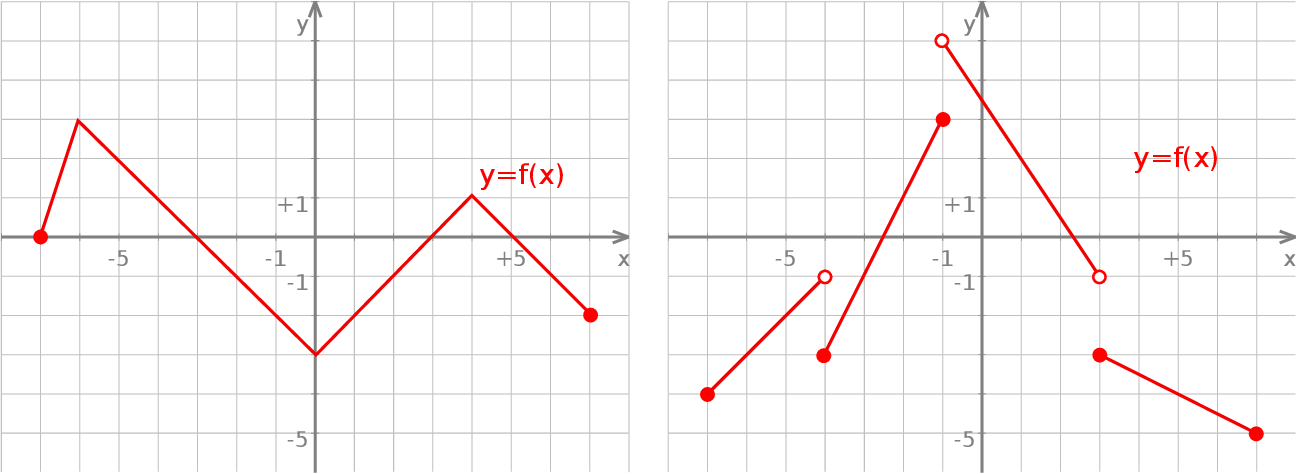
Funkcja przedstawiona na prawym wykresie rośnie na przedziałach 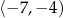 ,
, 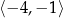 oraz maleje na przedziale
oraz maleje na przedziale 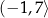 .
.
Zauważmy, że ta funkcja nie jest rosnąca na przedziale 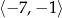 , bo dla
, bo dla 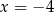 funkcja „przeskakuje w dół”.
funkcja „przeskakuje w dół”.

