/Szkoła średnia/Funkcje

Zadanie nr 2921481

Dodaj do ulubionych
Dodaj do rozwiązanych

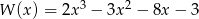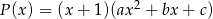Dane są wielomiany 3 2 W (x) = 2x − 3x − 8x − 3 i 2 P(x) = (x + 1 )(ax + bx + c) .

  • Wyznacz współczynniki 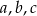a,b,c tak, aby W (x) = P (x) .
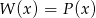  • Przedstaw wielomian 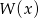W (x) jako iloczyn wielomianów liniowych.

Rozwiązanie

  •  

    Sposób I

    Wymnażamy czynniki wielomianu P(x ) .

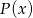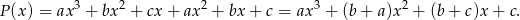
    3 2 2 3 2 P(x ) = ax + bx + cx + ax + bx + c = ax + (b+ a)x + (b+ c)x+ c.

    Daje to nam równość

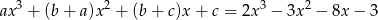
    ax3 + (b+ a)x2 + (b+ c)x+ c = 2x3 − 3x2 − 8x − 3

    Dwa wielomiany są równe jeżeli mają takie same współczynniki, czyli musi być 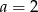a = 2 (patrząc na współczynnik przy 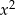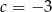x2 ), c = − 3 (patrząc na wyraz wolny). To daje b = − 5 .

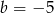    Sposób II

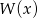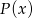    Skoro wielomiany W (x) i P (x) mają być równe to wielomian 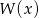W (x ) musi się dzielić przez 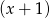(x + 1 ) . Podzielmy go (my robimy to grupując wyrazy).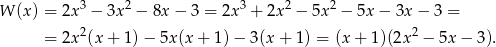

    W (x) = 2x 3 − 3x 2 − 8x− 3 = 2x3 + 2x 2 − 5x 2 − 5x− 3x − 3 = 2 2 = 2x (x+ 1)− 5x(x + 1) − 3(x + 1) = (x + 1 )(2x − 5x − 3).

    W takim razie a = 2 , b = − 5 , c = − 3 .  
    Odpowiedź: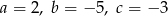 a = 2, b = − 5, c = − 3

  • Z poprzedniego podpunktu wiemy, że
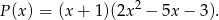
    2 P(x) = (x + 1 )(2x − 5x − 3).

    Pozostało więc rozłożyć trójmian w nawiasie.

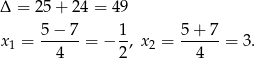
    Δ = 25 + 24 = 4 9 5−--7- 1- 5+--7- x1 = 4 = − 2 , x2 = 4 = 3.

    Zatem

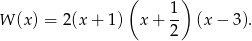
    ( 1) W (x) = 2(x + 1) x + -- (x − 3). 2

     
    Odpowiedź: ( ) W (x) = 2(x + 1) x + 1 (x− 3) 2

Wersja PDF