Nie dość, że funkcje trygonometryczne są trudne same w sobie, to zabawę z trygonometrią komplikuje się jeszcze bardziej i każe się zamiast stopni pisać radiany. Są jednak ku temu poważne powody i zanim powiemy jak dokładnie się definiuje radiany, spróbujmy wyjaśnić po co się je wprowadza. Historia funkcji trygonometrycznych Pierwsza obserwacja jest taka, że definicje funkcji trygonometrycznych w trójkącie prostokątnym pozwalają mówić tylko o funkcjach kątów ostrych. To jest za mało. Nawet jeżeli chcemy się zajmować tylko trójkątami, to przecież kąty w trójkącie mogą być rozwarte, a chcielibyśmy mieć twierdzenia sinusów czy cosinusów dla dowolnych trójkątów. Jak się jeszcze chwilę zastanowimy to w czworokątach, które nie są wypukłe, kąty mogą być dowolnie bliskie 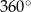 , więc potrzebujemy mieć funkcje trygonometryczne dowolnych kątów z przedziału
, więc potrzebujemy mieć funkcje trygonometryczne dowolnych kątów z przedziału 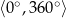 .
.
Jak się jeszcze trochę pobawimy funkcjami trygonometrycznymi, to odkrywamy różne wzory np.
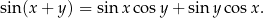
Jeżeli jednak umiemy liczyć funkcje trygonometryczne tylko w przedziale 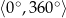 , to mamy dziwną sytuację, bo np. dla
, to mamy dziwną sytuację, bo np. dla 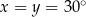 wzór jest OK, ale dla
wzór jest OK, ale dla 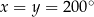 jest źle, bo z lewej strony wychodzimy poza dziedzinę sinusa.
jest źle, bo z lewej strony wychodzimy poza dziedzinę sinusa.
Kątowi 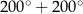 można jednak nadać interpretację geometryczną – jeżeli myślimy o ramieniu zaczepionym w punkcie
można jednak nadać interpretację geometryczną – jeżeli myślimy o ramieniu zaczepionym w punkcie  i obracającym się najpierw o
i obracającym się najpierw o 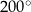 , a potem jeszcze raz o
, a potem jeszcze raz o 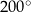 , to powinno być jasne, że jest to to samo, co jeden obrót tego ramienia o
, to powinno być jasne, że jest to to samo, co jeden obrót tego ramienia o 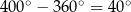 .
.
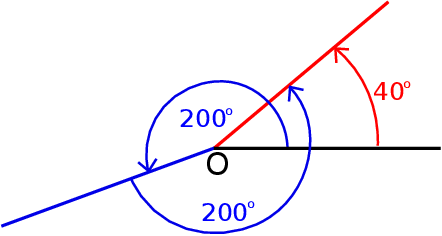
W ten sposób dochodzimy do tego, żeby zdefiniować
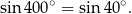
I tak dalej. W ten sposób definiujemy funkcje trygonometryczne dla dowolnych kątów. Liczby zamiast stopni Powyższe definicje funkcji trygonometrycznych dowolnych kątów mają jednak zasadniczą wadę: argumenty tych funkcji (to co do nich wstawiamy) nie są liczbami, tylko są liczbami z mianem (są to wielokrotności jednostki 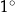 ). Np. nie ma sensu pytać się czy
). Np. nie ma sensu pytać się czy 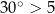 , albo liczyć
, albo liczyć 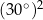 (można za to policzyć
(można za to policzyć 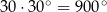 ). To jest duży problem, bo w ten sposób nie możemy robić z funkcjami trygonometrycznymi tego, co robimy z innymi funkcjami, na przykład nie mają sensu wyrażenia postaci
). To jest duży problem, bo w ten sposób nie możemy robić z funkcjami trygonometrycznymi tego, co robimy z innymi funkcjami, na przykład nie mają sensu wyrażenia postaci
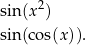
Pierwsze wyrażenie nie ma sensu, bo nie możemy mnożyć kątów przez siebie, a drugie bo do sinusa mamy wstawiać kąty, a nie liczby. Mówiąc jeszcze inaczej, chcemy myśleć o funkcji jak o maszynce, która zamienia liczby na liczby, a nie stopnie na liczby.
Aby rozwiązać ten problem, zamienia się kąty na liczby – i to są właśnie radiany, lub jak ktoś woli miara łukowa. Definicja miary łukowej Jak przyporządkować kątowi liczbę? – pomysł jest prosty: bierzemy okrąg jednostkowy (o promieniu długości 1), umieszczamy wierzchołek kąta w środku okręgu i patrzymy jaka jest długość łuku okręgu wyciętego przez ten kąt.

Ponieważ cały okrąg jednostkowy ma długość 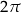 , to
, to
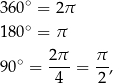
i tak dalej. Dla kątów spoza przedziału 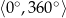 , wygodnie jest myśleć o długości łuku jaki zakreśla promień okręgu obracający się o dany kąt. Np. promień po obrocie o
, wygodnie jest myśleć o długości łuku jaki zakreśla promień okręgu obracający się o dany kąt. Np. promień po obrocie o 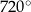 dwa razy odjedzie okrąg, więc
dwa razy odjedzie okrąg, więc 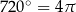 .
.
Ogólnie mamy wzór
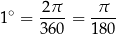
czyli
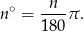
Ujemne kąty We wcześniejszej opowieści o definiowaniu funkcji trygonometrycznych dowolnych kątów pozostała istotna luka: nie powiedzieliśmy jak definiować funkcje trygonometryczne kątów ujemnych. A co to są kąty ujemne? – hm, tak naprawdę takich nie ma, musimy je dopiero wymyślić.
Jaką interpretację nadać kątowi 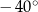 ? – odpowiedź jest prosta, ma to być taki kąt, żeby
? – odpowiedź jest prosta, ma to być taki kąt, żeby
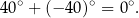
Jak coś takiego zrobić? – żaden problem: jeżeli myślimy o kącie 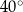 jako o kącie zakreślonym przez obracające się ramię zaczepione w punkcie
jako o kącie zakreślonym przez obracające się ramię zaczepione w punkcie  , to definiujemy kąt
, to definiujemy kąt  tak samo, ale ramię ma się kręcić w drugą stronę.
tak samo, ale ramię ma się kręcić w drugą stronę.
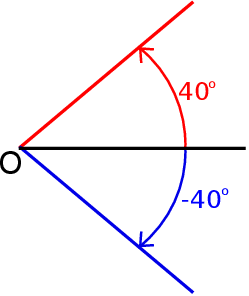
Jak dodamy do siebie takie kąty, to ramię najpierw obraca się o  , potem obraca się o ten sam kąt w drugą stronę, czyli w sumie nic się nie zmienia – wychodzi kąt
, potem obraca się o ten sam kąt w drugą stronę, czyli w sumie nic się nie zmienia – wychodzi kąt 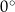 .
.
W ten sposób otrzymujemy definicję kątów zorientowanych, czyli takich, które mogą być dodatnie lub ujemne. Zauważmy, że tak naprawdę obu kątom 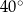 i
i 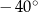 odpowiada ten sam kąt niezorientowany, czyli kawałek płaszczyzny między ramionami kąta.
odpowiada ten sam kąt niezorientowany, czyli kawałek płaszczyzny między ramionami kąta.
Różnica między kątami zorientowanymi i niezorientowanymi jest dokładnie taka sama jak różnica między odcinkami, a wektorami: wektor to odcinek, w którym wyróżniono jeden z końców (początek wektora); podobnie kąt zorientowany to kąt, w którym wyróżniono jedno z ramion (początkowe ramię kąta).
No to już sobie wyjaśniliśmy, co to są ujemne kąty, ale wciąż nie powiedzieliśmy jak zdefiniować 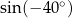 . Aby to zrobić, zauważmy, że ramię obrócone o kąt
. Aby to zrobić, zauważmy, że ramię obrócone o kąt 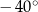 ląduje dokładnie w tym samym miejscu co ramię obrócone o
ląduje dokładnie w tym samym miejscu co ramię obrócone o 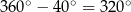 .
.
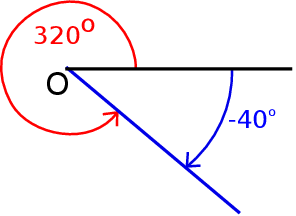
Definiujemy więc
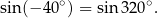
Orientacja płaszczyzny Kilka razy mówiliśmy już o obracaniu się promienia/półprostej o kąt. Jednak na płaszczyźnie możemy kręcić się w dwie strony: zgodnie z ruchem wskazówek zegara i przeciwnie. Aby mówić o kątach zorientowanych trzeba się umówić, który obrót ma być dodatni, a który ujemny. Ta umowa to tak zwany wybór orientacji płaszczyzny. Standardowo umawiamy się, że obrót przeciwny do ruchu wskazówek zegara jest dodatni, a obrót zgodny z ruchem wskazówek zegara jest ujemny. Oczywiście to tylko umowa, równie dobrze można by umówić się przeciwnie (czyli wybrać inną orientację płaszczyzny).
Tips & Tricks
1Podanego wzoru
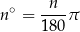
nie warto się uczyć na pamięć. Wystarczy zapamiętać, że 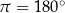 i wyliczać interesujący nas kąt z proporcji.
i wyliczać interesujący nas kąt z proporcji.
Zamieńmy kąt 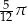 na stopnie.
na stopnie.
Mamy proporcję
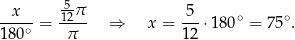
2Tak naprawdę w zadaniach szkolnych w kółko przewija się tylko kilka kątów:
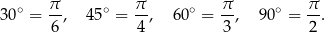
Jeżeli uda nam się zapamiętać te wartości (co tak czy inaczej się stanie, jeżeli będziemy rozwiązywać zadania z trygonometrii), to bez trudu będziemy wtedy identyfikować wielokrotności tych kątów, np.
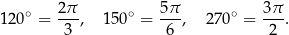
3Miarę łukową możemy również liczyć, jeżeli mamy kąt umieszczony w okręgu o dowolnym promieniu  – wtedy wystarczy popatrzeć jaką część długości całego okręgu on wycina.
– wtedy wystarczy popatrzeć jaką część długości całego okręgu on wycina.
Obliczmy miarę kąta środkowego w okręgu o promieniu 5, który wycina z tego okręgu łuk długości 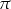 .
.
Cały okrąg ma długość 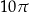 , zatem dany kąt stanowi
, zatem dany kąt stanowi 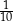 kąta pełnego, czyli ma miarę łukową
kąta pełnego, czyli ma miarę łukową
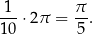
4Czasami wygodnie jest wyznaczać miarę łukową kąta środkowego patrząc nie na długość łuku jaki on wycina, ale sprawdzając jaką część pola wycina on z całego koła.
Obliczmy miarę łukową kąta środkowego w okręgu o promieniu 3, dla którego odpowiadający wycinek kołowy ma pole 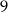 .
.
Pole całego koła jest równe 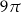 , zatem dany kąt stanowi
, zatem dany kąt stanowi 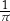 kąta pełnego, czyli jego miara łukowa jest równa
kąta pełnego, czyli jego miara łukowa jest równa
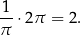
5Warto pamiętać, że miara kąta wpisanego w okrąg jest dwa razy mniejsza od miary kąta środkowego opartego na tym samym łuku.
Obliczmy miarę kąta wpisanego w okrąg o promieniu 5 opartego na łuku długości 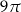 .
.
Cały okrąg ma długość 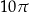 , zatem kąt środkowy oparty na danym łuku ma miarę łukową:
, zatem kąt środkowy oparty na danym łuku ma miarę łukową:
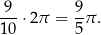
Kąt wpisany jest dwa razy mniejszy, więc ma miarę  .
.
6Nie należy zapominać, że miary kątów w radianach to prawdziwe liczby (w końcu o to chodziło!), więc 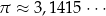 itd.
itd.
Oblicz 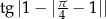 .
.
Liczymy
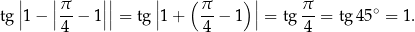
Rozwiążmy równanie 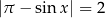
Ponieważ 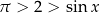 to możemy opuścić wartość bezwzględną:
to możemy opuścić wartość bezwzględną:
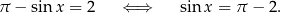
To jednak nie jest możliwe, bo prawa strona jest większa od 1, czyli równanie jest sprzeczne.
7Wprawdzie większość kątów, które przewijają się przez zadania szkolne ma w sobie 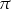 , ale oczywiście każda liczba rzeczywista wyznacza dokładnie jeden kąt.
, ale oczywiście każda liczba rzeczywista wyznacza dokładnie jeden kąt.
Jak wyobrazić sobie kąt o mierze 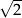 ?
?
Przesuwamy wzdłuż okręgu jednostkowego punkt o 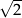 . Kąt jaki zakreśli odcinek łączący ten punkt ze środkiem okręgu to dokładnie kąt o mierze łukowej
. Kąt jaki zakreśli odcinek łączący ten punkt ze środkiem okręgu to dokładnie kąt o mierze łukowej 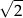 . Oczywiście to przesuwanie możemy sobie tylko wyobrazić – raczej nie uda nam się tego wykonać tego przy pomocy cyrkla i linijki.
. Oczywiście to przesuwanie możemy sobie tylko wyobrazić – raczej nie uda nam się tego wykonać tego przy pomocy cyrkla i linijki.
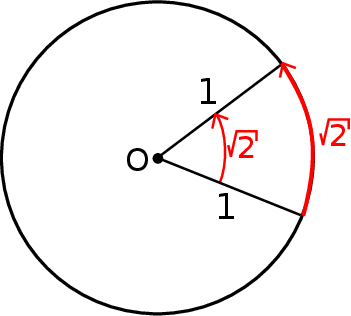
8Dlaczego zamieniając miarę kątów w stopniach na liczby (motywacja do wprowadzenia radianów) nie mogliśmy po prostu odrzucić stopni i mówić, że  to 360? Szczerze mówiąc mogliśmy, ale to jest gorsze niż radiany. Aby to wyjaśnić, musimy sobie uświadomić, co oznaczają liczby bez miana (bez jednostki). To jest trudny moment i historycznie pozbycie się jednostek zmieniło oblicze matematyki. Ustalamy, że wiemy co znaczy 1 – powiedzmy, że jest to długość jednostkowego odcinka na płaszczyźnie, np. długości 1cm. Jest jasne co w takiej sytuacji oznacza dodawanie i odejmowanie liczb. Kłopot zaczyna się z mnożeniem. Możemy o nim myśleć na trzy sposoby. O
to 360? Szczerze mówiąc mogliśmy, ale to jest gorsze niż radiany. Aby to wyjaśnić, musimy sobie uświadomić, co oznaczają liczby bez miana (bez jednostki). To jest trudny moment i historycznie pozbycie się jednostek zmieniło oblicze matematyki. Ustalamy, że wiemy co znaczy 1 – powiedzmy, że jest to długość jednostkowego odcinka na płaszczyźnie, np. długości 1cm. Jest jasne co w takiej sytuacji oznacza dodawanie i odejmowanie liczb. Kłopot zaczyna się z mnożeniem. Możemy o nim myśleć na trzy sposoby. O  można myśleć tak: że trzy razy bierzemy odcinek długości 5 (czyli
można myśleć tak: że trzy razy bierzemy odcinek długości 5 (czyli  ), że 5 razy bierzemy odcinek długości 3 (czyli
), że 5 razy bierzemy odcinek długości 3 (czyli  ), lub że liczymy pole prostokąta o bokach 3 i 5 (czyli
), lub że liczymy pole prostokąta o bokach 3 i 5 (czyli 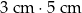 ). Tak się szczęśliwie składa, że za każdym razem wychodzi to samo i dlatego piszemy
). Tak się szczęśliwie składa, że za każdym razem wychodzi to samo i dlatego piszemy 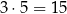 nie przejmując się co ten napis oznacza. Dzięki temu ma np. sens działanie
nie przejmując się co ten napis oznacza. Dzięki temu ma np. sens działanie 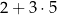 i nie musimy się zastanawiać czy to przypadkiem nie jest dodawanie odcinka do prostokąta. Nie ma też kłopotów z interpretacją wyrażenia
i nie musimy się zastanawiać czy to przypadkiem nie jest dodawanie odcinka do prostokąta. Nie ma też kłopotów z interpretacją wyrażenia 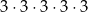 , do którego jednostki możemy już dopisać na wiele sposobów.
, do którego jednostki możemy już dopisać na wiele sposobów.
No to wracamy do radianów. Ustaliliśmy już, że na płaszczyźnie jest ustalona jednostka (np. 1 cm). Miara w stopniach zupełnie tę jednostkę ignoruje: 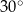 oznacza dokładnie to samo, gdy jednostką jest 1 cm i gdy jednostką jest 1 m. W takim razie, zamienienie
oznacza dokładnie to samo, gdy jednostką jest 1 cm i gdy jednostką jest 1 m. W takim razie, zamienienie 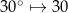 jest lekko bez sensu:
jest lekko bez sensu: 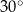 i 30 (wielokrotność jednostki) nie mają ze sobą nic wspólnego, np. otrzymana w ten sposób nierówność
i 30 (wielokrotność jednostki) nie mają ze sobą nic wspólnego, np. otrzymana w ten sposób nierówność 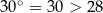 nie ma żadnej interpretacji geometrycznej, liczby po obu stronach pochodzą z zupełnie innych światów.
nie ma żadnej interpretacji geometrycznej, liczby po obu stronach pochodzą z zupełnie innych światów.
Inaczej jest z radianami. Przyporządkowanie kątowi długości łuku jaki on wycina z okręgu jednostkowego jak najbardziej uwzględnia przyjętą na płaszczyźnie jednostkę – można powiedzieć, że jest to mierzenie kątów tą samą miarką, którą mierzymy długości odcinków.
Z pewnością powyższy komentarz nie jest łatwy do zrozumienia (szczególnie przy pierwszym czytaniu), ale powinien co najmniej zostawić wrażenie, że są ważne powody wyższości radianów nad stopniami.
9Podobnie jak dla kątów na płaszczyźnie, można próbować mierzyć kąty bryłowe (przestrzenne) polem powierzchni jaki ma obszar wycięty przez nie ze sfery o promieniu 1. Tu jednak sytuacja jest bardziej skomplikowana i taka miara nie jest aż tak użyteczna jak miara łukowa na płaszczyźnie. Powód jest taki, że jeżeli chcemy, żeby miara jednoznacznie wyznaczała kąt z dokładnością do przesunięcia i obrotu, to musimy się ograniczyć do okrągłych kątów jakie tworzą stożki. Jednak najciekawsze kąty przestrzenne to kąty wielościenne (takie jak otoczenie wierzchołka ostrosłupa). Takie kąty na ogół mierzy się miarami kątów płaskich pomiędzy tworzącymi go półprostymi.

