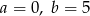/Szkoła średnia/Funkcje

Zadanie nr 3074904

Dodaj do ulubionych
Dodaj do rozwiązanych

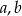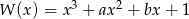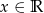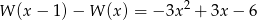Wyznacz współczynniki a,b wielomianu 3 2 W (x) = x + ax + bx+ 1 wiedząc, że dla każdego x ∈ R prawdziwa jest równość: W (x − 1) − W (x ) = − 3x2 + 3x − 6 .

Rozwiązanie

Liczymy

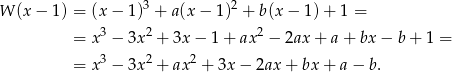
3 2 W (x − 1) = (x− 1) + a (x− 1) + b (x− 1)+ 1 = = x3 − 3x2 + 3x − 1 + ax2 − 2ax + a + bx − b + 1 = 3 2 2 = x − 3x + ax + 3x − 2ax + bx + a− b .

Stąd

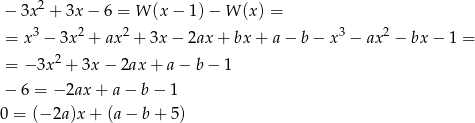
− 3x 2 + 3x − 6 = W (x − 1) − W (x ) = 3 2 2 3 2 = x − 3x + ax + 3x − 2ax + bx + a− b− x − ax − bx− 1 = 2 = − 3x + 3x − 2ax + a − b − 1 − 6 = − 2ax+ a− b− 1 0 = (− 2a)x + (a − b+ 5)

Skoro funkcja liniowa ma być stale równa 0, oba jej współczynniki muszą być zerami. Daje to nam układ równań.

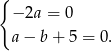
{ − 2a = 0 a− b+ 5 = 0.

Stąd 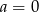a = 0 i b = 5 .  
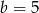Odpowiedź: a = 0 , b = 5

Wersja PDF