Zadanie nr 3256127

Wykaż, że wszystkie wartości funkcji 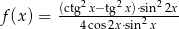(ctg2x−tg2x)⋅sin22x f(x) = ---4cos2x⋅sin2x---- są większe od 1.

Rozwiązanie

Korzystając ze wzorów

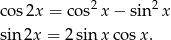
2 2 co s2x = cos x − sin x sin 2x = 2 sinx cos x.

przekształcimy podane wyrażenie.

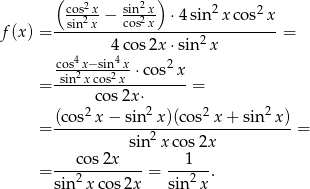
( ) cos22x-− -sin22x ⋅4 sin 2x cos2x f(x) = --sin-x---cos-x-----------------= 4co s2x ⋅sin2x cos4x−sin4x- 2 = -sin2xcos2x-⋅cos--x = cos2x ⋅ (cos2 x− sin 2x)(cos2 x+ sin 2x) = -------------2-------------------= sin xcos 2x ---cos-2x--- --1--- = sin2x cos 2x = sin 2x.

Wartość danej funkcji będzie zatem najmniejsza, gdy mianownik, czyli 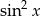sin2x będzie największy, czyli równy 1.

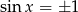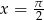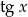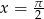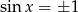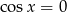Koniecznie trzeba jednak zwrócić uwagę na bardzo delikatny moment. W jakim punkcie funkcja przyjmuje tę najmniejszą wartość? W pierwszej chwili mogło by się wydawać, że w każdym, w którym sin x = ± 1 , czyli np. w x = π- 2 . To jest jednak źle, bo w oryginalnym wzorze funkcji jest funkcja tgx i nie należy do dziedziny tej funkcji. Co więcej, zawsze gdy to cos x = 0 (z jedynki trygonometrycznej). Zatem podana funkcja osiąga wartości dowolnie bliskie 1, ale nigdy nie przyjmuje wartości 1. To oznacza, że 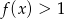f (x) > 1 dla dowolnego z dziedziny funkcji.