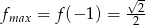Zadanie nr 3355576
Wyznacz największą wartość funkcji 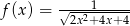 .
.
Rozwiązanie
Zacznijmy od sprawdzenia jaka jest dziedzina podanej funkcji. Liczymy 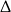 -ę wyrażenia pod pierwiastkiem.
-ę wyrażenia pod pierwiastkiem.
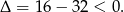
Zatem 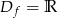 .
.
Wartość ułamka będzie największa, gdy mianownik będzie najmniejszy, więc wystarczy znaleźć najmniejszą wartość funkcji 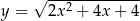 . Ponadto pierwiastek jest funkcją rosnącą, więc wystarczy zajmować się funkcją
. Ponadto pierwiastek jest funkcją rosnącą, więc wystarczy zajmować się funkcją 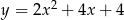 . Wykresem tej funkcji jest parabola o ramionach skierowanych w górę i wierzchołku w punkcie
. Wykresem tej funkcji jest parabola o ramionach skierowanych w górę i wierzchołku w punkcie 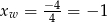 . Wartość w tym punkcie to
. Wartość w tym punkcie to
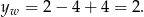
Zatem największa wartość funkcji 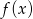 to
to
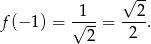
Odpowiedź: