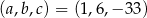/Szkoła średnia/Funkcje

Zadanie nr 3619869

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametrów 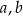a,b i c , dla których wielomian

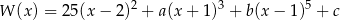
2 3 5 W (x) = 25(x − 2) + a(x + 1) + b (x − 1) + c

jest podzielny przez wielomian 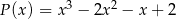3 2 P (x) = x − 2x − x + 2 .

Rozwiązanie

Zobaczmy jakie pierwiastki ma wielomian przez który dzielimy.

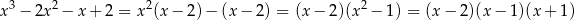
3 2 2 2 x − 2x − x + 2 = x (x− 2)− (x − 2) = (x − 2)(x − 1) = (x − 2)(x − 1)(x + 1)

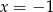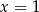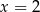Na mocy twierdzenia Bézout wystarczy sprawdzić, kiedy liczby x = − 1 , x = 1 i x = 2 są pierwiastkami podanego wielomianu 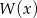W (x ) . Sprawdzamy.

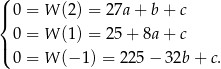
(| 0 = W (2) = 27a + b + c { 0 = W (1) = 25 + 8a + c |( 0 = W (− 1) = 225 − 3 2b+ c.

Odejmujemy od pierwszego równania drugie i od drugiego trzecie.

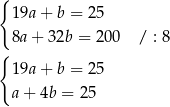
{ 19a + b = 2 5 8a + 32b = 200 / : 8 { 19a + b = 2 5 a+ 4b = 25

Podstawiamy teraz 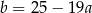b = 25 − 19a z pierwszego równania do drugiego.

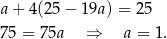
a + 4 (2 5− 19a) = 25 7 5 = 75a ⇒ a = 1.

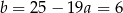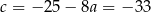Stąd b = 25 − 19a = 6 i c = − 25 − 8a = −3 3 .  
Odpowiedź: (a,b,c) = (1 ,6,− 33)

Wersja PDF