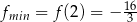/Szkoła średnia/Funkcje

Zadanie nr 3668910

Dodaj do ulubionych
Dodaj do rozwiązanych

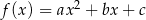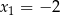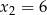Funkcja kwadratowa 2 f(x ) = ax + bx + c ma dwa miejsca zerowe x 1 = − 2 i x2 = 6 . Wykres funkcji 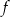f przechodzi przez punkt 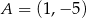A = (1,− 5) . Oblicz najmniejszą wartość funkcji f .

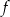Rozwiązanie

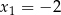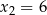Trójmian o pierwiastkach x 1 = − 2 i x2 = 6 ma postać iloczynową

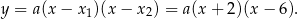
y = a(x − x1)(x − x2) = a(x+ 2)(x− 6).

Podstawiamy współrzędne punktu 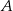A i wyznaczamy współczynnik a

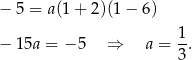
− 5 = a(1+ 2)(1− 6) 1 − 15a = − 5 ⇒ a = -. 3

Zatem trójmian ma postać iloczynową

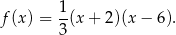
1- f(x) = 3(x + 2)(x − 6 ).

Wykresem tej funkcji jest parabola o ramionach skierowanych w górę i pierwszej współrzędnej wierzchołka

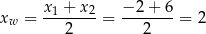
x1 +-x2- −-2+-6- xw = 2 = 2 = 2

(wierzchołek zawsze znajduje się w środku pomiędzy pierwiastkami). W takim razie wartość najmniejsza funkcji to

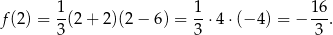
1 1 16 f(2) = -(2 + 2)(2 − 6) = --⋅4⋅(− 4) = − --. 3 3 3

Na koniec wykres dla ciekawskich.

PIC

 
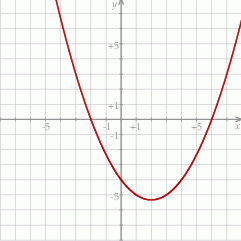
Odpowiedź: fmin = f(2) = − 163

Wersja PDF