/Szkoła średnia/Funkcje

Zadanie nr 3850927

Dodaj do ulubionych
Dodaj do rozwiązanych

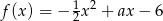Dana jest rodzina funkcji kwadratowych zmiennej rzeczywistej x , opisana wzorem f(x ) = − 12x2 + ax − 6 , gdzie a jest liczbą rzeczywistą.

  • Dla 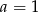a = 1 wyznacz zbiór tych argumentów, dla których funkcja 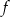f przyjmuje wartości większe niż funkcja liniowa g(x) = x − 8 .
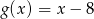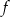  • Wyznacz liczbę a , dla której zbiorem wartości funkcji f jest przedział (− ∞ ,0⟩ .
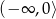  • Dla 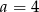a = 4 napisz wzór funkcji 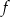f w postaci kanonicznej i narysuj jej wykres.

Rozwiązanie

  • Zapiszmy wzór funkcji 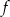f dla a = 1
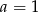
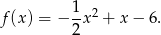
    f(x) = − 1-x2 + x− 6. 2

    Szukamy argumentów dla których funkcja 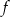f jest większa od 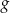g , czyli rozwiązujemy nierówność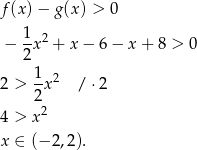

    f(x )− g (x) > 0 1 2 − -x + x− 6− x+ 8 > 0 2 2 > 1x2 /⋅ 2 2 4 > x 2 x ∈ (− 2,2).

     
    Odpowiedź: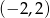 (− 2,2)

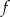  • Zauważmy, że dla każdego a wykres funkcji f jest parabolą z ramionami skierowanymi w dół. Zatem zbiór wartości funkcji 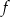f to przedział 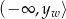(− ∞ ,y ⟩ w , gdzie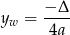
    − Δ yw = ---- 4a

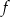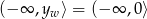    jest drugą współrzędną wierzchołka paraboli będącej wykresem funkcji f . Szukamy wartości a , dla której (− ∞ ,yw ⟩ = (− ∞ ,0⟩ . Tak będzie, gdy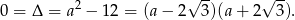

    √ -- √ -- 0 = Δ = a 2 − 12 = (a− 2 3)(a + 2 3).

     
    Odpowiedź: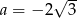 √ -- a = − 2 3 lub √ -- a = 2 3

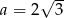
  • Zapiszmy wzór funkcji 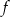f dla a = 4
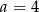
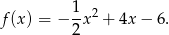
    1 2 f(x ) = − -x + 4x − 6 . 2

    Postać kanoniczną wyznaczymy na dwa sposoby.

    Sposób I

    Wyznaczamy współrzędne wierzchołka

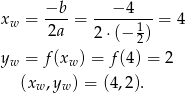
    −b − 4 xw = ----= ------1-= 4 2a 2⋅(− 2) yw = f(xw ) = f(4) = 2 (xw,yw ) = (4,2).

    Teraz możemy już zapisać w postaci kanonicznej

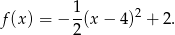
    1 2 f(x) = − --(x − 4) + 2. 2

    Sposób II

    Przekształcamy wzór funkcji 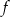f do postaci kanonicznej (zwijamy do kwadratu).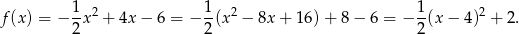

    1 1 1 f(x ) = − -x 2 + 4x − 6 = − -(x 2 − 8x + 16)+ 8− 6 = − -(x − 4 )2 + 2. 2 2 2

    Na koniec rysujemy wykres funkcji 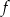f – jest to parabola 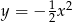1 2 y = − 2x przesunięta o 4 jednostki w prawo i dwie do góry.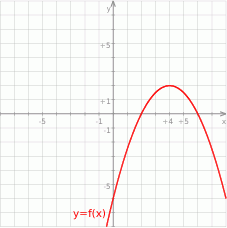

    PIC

     
    Odpowiedź: 1 2 f(x) = − 2(x− 4) + 2

Wersja PDF