/Szkoła średnia/Funkcje

Zadanie nr 3929382

Dodaj do ulubionych
Dodaj do rozwiązanych

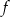Funkcja f określona jest wzorem 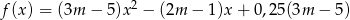2 f(x ) = (3m − 5 )x − (2m − 1)x + 0 ,25(3m − 5) . Wyznacz te wartości parametru 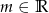m ∈ R , dla których najmniejsza wartość funkcji 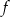f jest liczbą dodatnią.

Rozwiązanie

Sprawdźmy najpierw co się dzieje, gdy funkcja jest liniowa, czyli dla 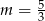5 m = 3 . Mamy wtedy funkcję 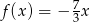f (x) = − 73x i oczywiście nie spełnia ona żądanego warunku.

Możemy zatem założyć, że wykres podanej funkcji jest parabolą. Ponadto, aby istaniała wartość najmniejsza jej ramiona muszą być skierowane do góry, czyli 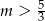5 m > 3 . W takiej sytuacji najmniejsza wartość jest osiągana w wierzchołku paraboli, musimy więc sprawdzić, kiedy jest on powyżej osi 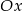Ox . Najprościej jest to zrobić licząc 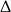Δ -ę (funkcja ma nie mieć pierwiastków).

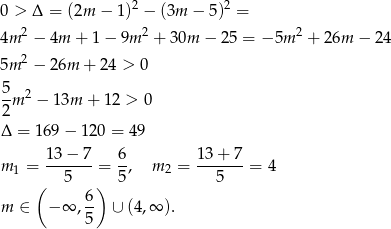
0 > Δ = (2m − 1)2 − (3m − 5)2 = 2 2 2 4m − 4m + 1− 9m + 3 0m − 2 5 = − 5m + 2 6m − 2 4 5m 2 − 26m + 24 > 0 5-m 2 − 1 3m + 1 2 > 0 2 Δ = 169 − 12 0 = 49 m = 1-3−--7 = 6-, m = 13-+-7-= 4 1 ( 5 ) 5 2 5 6 m ∈ − ∞ ,-- ∪ (4 ,∞ ). 5

Uwzględniając nierówność 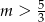5 m > 3 , mamy

m ∈ (4,∞ ).

 
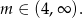
Odpowiedź: (4,+ ∞ )

Wersja PDF