Zadanie nr 3962819
Wielomian 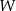 dany jest wzorem
dany jest wzorem 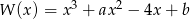 .
.
- Wyznacz
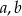 oraz
oraz  tak, aby wielomian
tak, aby wielomian 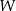 był równy wielomianowi
był równy wielomianowi 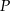 , gdy
, gdy 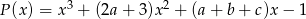 .
. - Dla
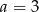 i
i 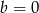 zapisz wielomian
zapisz wielomian 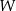 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Rozwiązanie
- Dwa wielomiany są równe jeżeli mają identyczne współczynniki. Daje to nam układ równań
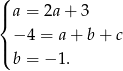
Z ostatniego równania mamy
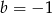 , z pierwszego
, z pierwszego 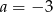 , zatem drugie przyjmuje postać
, zatem drugie przyjmuje postać 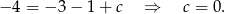
Odpowiedź: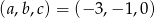
- Dla podanych wartości
 i
i 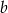 mamy wielomian
mamy wielomian 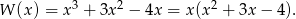
Pozostało teraz rozłożyć trójmian w nawiasie.
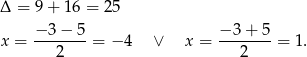
Mamy więc
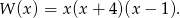
Odpowiedź: