Zadanie nr 4251133
Maksymalny przedział, na którym funkcja 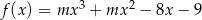 jest malejąca ma długość 2. Oblicz wartość parametru
jest malejąca ma długość 2. Oblicz wartość parametru 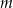 oraz wyznacz największą wartość funkcji na przedziale
oraz wyznacz największą wartość funkcji na przedziale 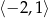 .
.
Rozwiązanie
Jeżeli 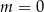 , to funkcja
, to funkcja 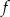 jest funkcją liniową i oczywiście nie może spełniać podanego warunku. Zatem
jest funkcją liniową i oczywiście nie może spełniać podanego warunku. Zatem 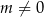 i mamy do czynienia z wielomianem stopnia 3. Pochodna tego wielomianu
i mamy do czynienia z wielomianem stopnia 3. Pochodna tego wielomianu
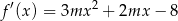
jest funkcją kwadratową, której znak decyduje o monotoniczności funkcji 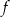 . W takim razie rozwiązaniem nierówności
. W takim razie rozwiązaniem nierówności 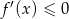 musi być przedział
musi być przedział 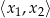 długości 2. W szczególności
długości 2. W szczególności 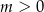 i
i 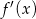 musi mieć dwa pierwiastki, czyli
musi mieć dwa pierwiastki, czyli
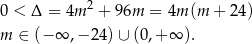
Ponadto pierwiastki 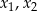 trójmianu
trójmianu 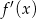 muszą spełniać warunek
muszą spełniać warunek
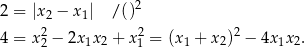
Korzystamy teraz ze wzorów Viète’a.
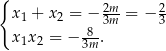
Mamy zatem równanie
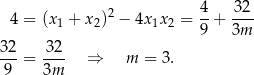
Zatem 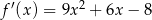 . Wyznaczmy jeszcze miejsca zerowe pochodnej – będzie nam to potrzebne do wyznaczenia największej wartości funkcji.
. Wyznaczmy jeszcze miejsca zerowe pochodnej – będzie nam to potrzebne do wyznaczenia największej wartości funkcji.
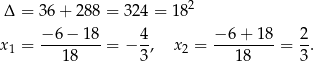
To oznacza, że pochodna jest dodatnia na przedziałach 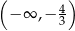 ,
, 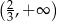 oraz ujemna na przedziale
oraz ujemna na przedziale 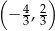 . Zatem funkcja
. Zatem funkcja 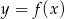 rośnie na przedziałach
rośnie na przedziałach 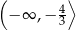 ,
, 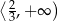 oraz maleje na przedziale
oraz maleje na przedziale 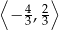 . W szczególności, w punkcie
. W szczególności, w punkcie 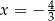 funkcja osiąga maksimum lokalne i największa wartość funkcji
funkcja osiąga maksimum lokalne i największa wartość funkcji 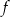 na przedziale
na przedziale 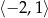 to albo
to albo 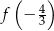 albo
albo 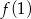 . Obliczamy obie wartości.
. Obliczamy obie wartości.
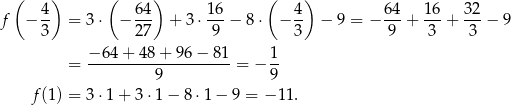
Oczywiście pierwsza z tych liczb stanowi największą wartość funkcji na przedziale 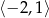 .
.
Na koniec wykres funkcji 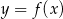 .
.
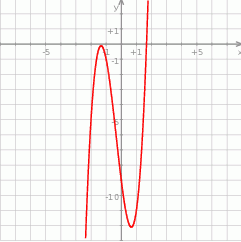
Odpowiedź: 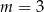 ,
,