Zadanie nr 4301143
Wyznacz zbiór wartości funkcji 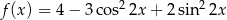 dla
dla 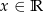 .
.
Rozwiązanie
Zauważmy najpierw, że
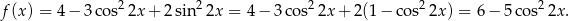
Sposób I
Ponieważ 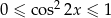 mamy nierówności
mamy nierówności
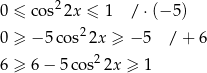
Sposób II
Korzystając ze wzoru
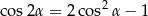
możemy zamienić 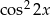 na
na 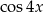 . Dzięki temu nie będzie kwadratu.
. Dzięki temu nie będzie kwadratu.
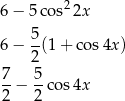
Korzystając teraz z nierówności 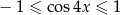 otrzymujemy tę samą odpowiedź co poprzednio.
otrzymujemy tę samą odpowiedź co poprzednio.
Sposób III
Pierwszy sposób rozwiązania możemy też zapisać używając podstawienia. Podstawiamy 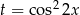 . Wtedy
. Wtedy 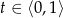 i szukamy zbioru wartości funkcji liniowej
i szukamy zbioru wartości funkcji liniowej 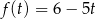 . Funkcja ta jest malejąca, więc jej zbiór wartości to przedział
. Funkcja ta jest malejąca, więc jej zbiór wartości to przedział
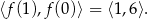
Odpowiedź: