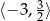Zadanie nr 4354385
Wyznacz zbiór wartości funkcji: 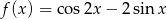 , gdzie
, gdzie 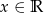 .
.
Rozwiązanie
Korzystamy ze wzoru na cosinus podwojonego kąta:
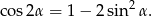
Mamy więc
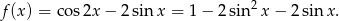
Jeżeli podstawimy teraz 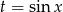 to mamy zwykłą funkcję kwadratową
to mamy zwykłą funkcję kwadratową
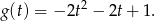
Musimy teraz zbadać jakie ona przyjmuje wartości na przedziale 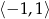 (bo takie wartości przyjmuje
(bo takie wartości przyjmuje 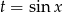 ). Sprawdźmy najpierw gdzie jest wierzchołek paraboli będącej wykresem funkcji
). Sprawdźmy najpierw gdzie jest wierzchołek paraboli będącej wykresem funkcji 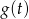 .
.
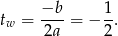
Ponieważ ramiona paraboli są skierowane w dół, oraz punkt ten jest w interesującym nas przedziale, dokładnie w tym punkcie otrzymamy największą wartość funkcji i jest ona równa
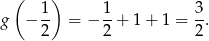
Wartość najmniejszą otrzymamy w jednym z końców przedziału, w którym? - liczymy i sprawdzamy.
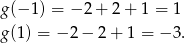
Odpowiedź: