/Szkoła średnia/Funkcje

Zadanie nr 4805719

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli 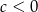c < 0 , to trójmian kwadratowy 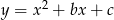2 y = x + bx + c ma dwa różne miejsca zerowe.

Rozwiązanie

Sposób I

Z założenia 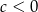c < 0 mamy

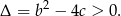
2 Δ = b − 4c > 0.

Zatem rzeczywiście dany trójmian ma dwa różne miejsca zerowe.

Sposób II

Jeżeli oznaczymy 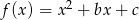f(x ) = x2 + bx + c to z założenia 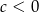c < 0 mamy

f (0) = c < 0.

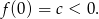
To oznacza, że wykresem funkcji 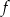f jest parabola o ramionach skierowanych w górę, której wierzchołek jest położony poniżej osi 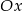Ox . Funkcja 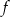f musi więc mieć dwa różne miejsca zerowe.

Wersja PDF