Zadanie nr 6523665
Oblicz wartość funkcji 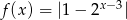 dla argumentu
dla argumentu
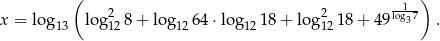
Rozwiązanie
Przekształćmy najpierw podane wyrażenie korzystając ze znanych własności logarytmów.
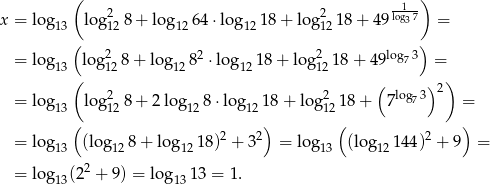
Zatem
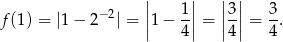
Odpowiedź: 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz wartość funkcji 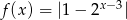 dla argumentu
dla argumentu
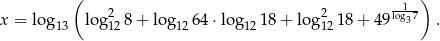
Przekształćmy najpierw podane wyrażenie korzystając ze znanych własności logarytmów.
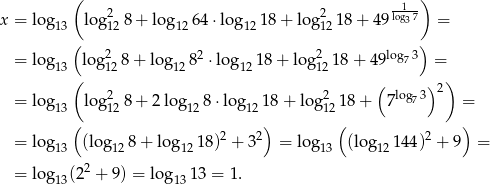
Zatem
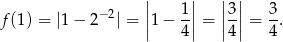
Odpowiedź: 
