Zadanie nr 7826231
Wyznacz resztę z dzielenia wielomianu 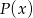 przez trójmian
przez trójmian 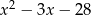 jeśli
jeśli 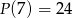 i
i 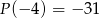 .
.
Rozwiązanie
Rozłóżmy trójmian 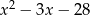 na czynniki.
na czynniki.
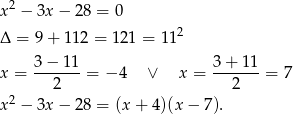
Reszta 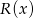 z dzielenia wielomianu
z dzielenia wielomianu 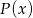 przez ten trójmian będzie wielomianem liniowym (bo reszta zawsze ma stopień mniejszy od stopnia wielomianu, przez który dzielimy) takim, że
przez ten trójmian będzie wielomianem liniowym (bo reszta zawsze ma stopień mniejszy od stopnia wielomianu, przez który dzielimy) takim, że
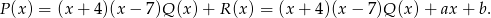
Współczynniki  i
i 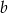 wyliczamy podstawiając w tej równości
wyliczamy podstawiając w tej równości 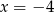 i
i 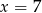 .
.
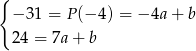
Odejmujemy od drugiego równania pierwsze (żeby zredukować 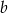 ) i mamy
) i mamy
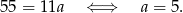
Zatem 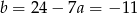 .
.
Odpowiedź: