/Szkoła średnia/Funkcje

Zadanie nr 7844094

Dodaj do ulubionych
Dodaj do rozwiązanych

Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.

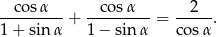
cos α cosα 2 ---------+ ---------= -----. 1 + sin α 1 − sinα cos α

Rozwiązanie

Przekształcamy lewą stronę danej równości tak, aby dojść do prawej strony.

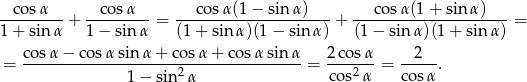
--cosα---+ --cosα---= ---cosα-(1−--sin-α)----+ ---cos-α(1-+-sinα-)---= 1 + sinα 1− sin α (1 + sinα )(1− sin α) (1 − sin α)(1+ sin α) cos α − cos αsin α+ cosα + co sαsin α 2co sα 2 = ---------------------2---------------- = ---2---= -----. 1 − sin α cos α cosα

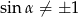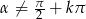Powyższy rachunek miał sens przy założeniu, że sin α ⁄= ± 1 , czyli α ⁄= π-+ kπ 2 , k ∈ Z .  
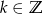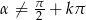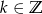Odpowiedź: Równość jest tożsamością przy założeniu: π- α ⁄= 2 + kπ , k ∈ Z .

Wersja PDF