Zadanie nr 8248408
Wiedząc, że 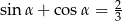 , oblicz
, oblicz 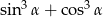 .
.
Rozwiązanie
Najpierw obliczymy 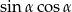 . W tym celu podnosimy równość
. W tym celu podnosimy równość
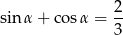
do kwadratu.
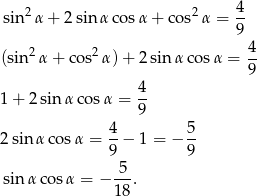
Teraz korzystamy ze wzoru na sumę sześcianów.
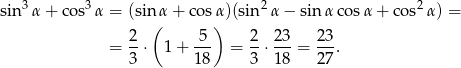
Odpowiedź: 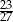
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiedząc, że 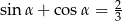 , oblicz
, oblicz 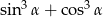 .
.
Najpierw obliczymy 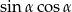 . W tym celu podnosimy równość
. W tym celu podnosimy równość
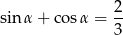
do kwadratu.
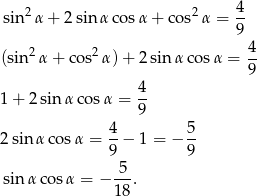
Teraz korzystamy ze wzoru na sumę sześcianów.
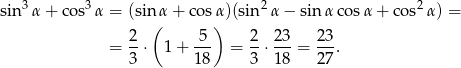
Odpowiedź: