/Szkoła średnia/Funkcje - wykresy/Parabola/Różne

Zadanie nr 1047525

Dla każdej liczby rzeczywistej 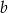b równanie 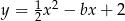1 2 y = 2x − bx + 2 opisuje pewną parabolę. Wyznacz wszystkie wartości parametru 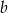b , dla których wierzchołek paraboli leży nad osią Ox .

Wersja PDF

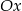Rozwiązanie

Korzystając ze wzoru na współrzędne wierzchołka paraboli wiemy, że druga współrzędna wierzchołka jest równa

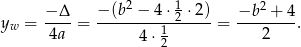
2 1 2 y = −-Δ- = −(b--−-4-⋅2-⋅2)-= −b--+--4. w 4a 4 ⋅ 1 2 2

Pozostało sprawdzić kiedy liczba ta jest dodatnia (bo dokładnie wtedy wierzchołek będzie leżał powyżej osi 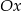Ox ).

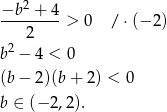
−b 2 + 4 --------> 0 / ⋅(− 2 ) 2 b 2 − 4 < 0 (b − 2)(b + 2) < 0 b ∈ (− 2 ,2 ).

 
Odpowiedź: b ∈ (− 2,2)

Wersja PDF