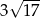/Szkoła średnia/Funkcje - wykresy/Parabola/Różne

Zadanie nr 1293914

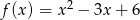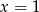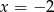Wykres funkcji kwadratowej f danej wzorem 2 f(x) = x − 3x + 6 przecięto prostymi o równaniach x = 1 oraz x = − 2 . Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji f .

Wersja PDF

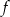Rozwiązanie

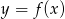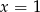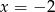Punkty wspólne wykresu funkcji y = f (x) z pionowymi prostymi x = 1 i x = − 2 to punkty o współrzędnych 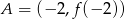A = (− 2,f(− 2)) i B = (1,f(1)) .

PIC

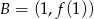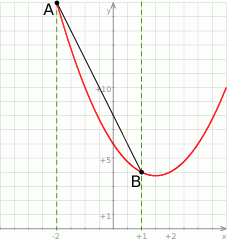
Ponieważ

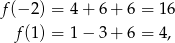
f(− 2) = 4 + 6 + 6 = 16 f(1) = 1 − 3 + 6 = 4,

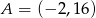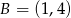mamy A = (− 2,16) i B = (1,4) . Pozostało teraz obliczyć długość odcinka AB .

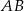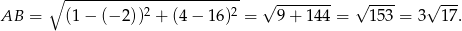
------------------------ ∘ 2 2 √ -------- √ ---- √ --- AB = (1 − (− 2)) + (4− 16) = 9 + 14 4 = 153 = 3 17.

 
Odpowiedź: √ --- 3 17

Wersja PDF