/Szkoła średnia/Funkcje - wykresy/Parabola/Różne

Zadanie nr 1755136

Dla jakich wartości parametru 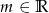m ∈ R wierzchołek paraboli 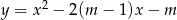2 y = x − 2(m − 1)x− m leży najbliżej osi Ox .

Wersja PDF

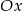Rozwiązanie

Obliczmy drugą współrzędną wierzchołka paraboli

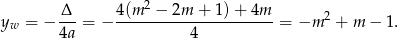
2 yw = − Δ--= − 4-(m--−-2m--+-1)-+-4m- = −m 2 + m − 1 . 4a 4

Wykresem otrzymanej funkcji zmiennej 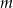m jest parabola o ramionach skierowanych w dół i wierzchołku w punkcie

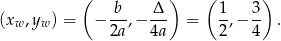
( ) ( ) (xw,yw ) = − b-,− -Δ- = 1,− 3- . 2a 4a 2 4

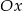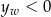Widać teraz, że wierzchołek danej paraboli leży zawsze poniżej osi Ox (bo yw < 0 ). Wierzchołek będzie najbliżej tej osi, gdy 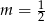m = 1 2 (wtedy wierzchołek jest najwyżej).  
Odpowiedź: 1 m = 2

Wersja PDF