Zadanie nr 4959143
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 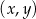 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 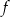 oraz
oraz 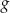 (zobacz rysunek).
(zobacz rysunek).
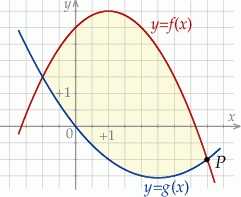
Funkcje 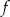 oraz
oraz 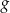 są określone wzorami
są określone wzorami 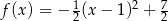 oraz
oraz  . Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt 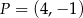 . Niech
. Niech 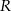 będzie punktem leżącym na wykresie funkcji
będzie punktem leżącym na wykresie funkcji 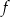 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 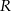 od punktu
od punktu 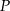 wyraża się wzorem
wyraża się wzorem
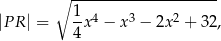
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 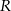 .
.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

