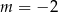/Szkoła średnia/Funkcje - wykresy/Parabola/Różne

Zadanie nr 8420762

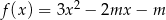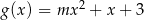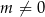Wykresy funkcji kwadratowych 2 f(x ) = 3x − 2mx − m oraz 2 g (x) = mx + x + 3 , dla m ⁄= 0 , przecinają się w dwóch punktach. Wyznacz wszystkie wartości 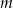m , dla których iloraz sumy odciętych tych punktów przez ich iloczyn jest o 18 mniejszy od największej wartości funkcji g .

Wersja PDF

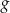Rozwiązanie

Spróbujmy wyznaczyć punkty wspólne podanych wykresów.

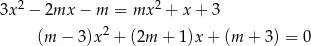
2 2 3x − 2mx − m = mx + x+ 3 (m − 3)x 2 + (2m + 1)x + (m + 3) = 0

Jeżeli wykresy mają przecinać się w dwóch punktach, to musi być spełniony warunek 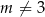m ⁄= 3 oraz

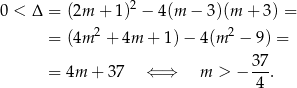
0 < Δ = (2m + 1 )2 − 4(m − 3)(m + 3) = = (4m 2 + 4m + 1) − 4(m 2 − 9) = 37 = 4m + 3 7 ⇐ ⇒ m > − ---. 4

Przy tych założeniach, równanie ma dwa rozwiązania 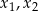x1,x2 i na mocy wzorów Viète’a.

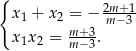
{ 2m +1 x1 + x2 = − m−-3- x1x2 = m+-3. m− 3

Potrzebujemy jeszcze największej wartości funkcji 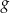g – jest to druga współrzędna 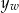yw wierzchołka jej wykresu, czyli liczba

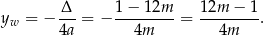
Δ 1− 1 2m 12m − 1 yw = − ---= − --------= ---------. 4a 4m 4m

Pozostało rozwiązać równanie

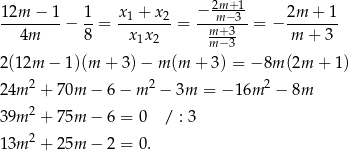
12m − 1 1 x + x − 2m+-1 2m + 1 ---------− --= -1----2-= ---m−3- = − ------- 4m 8 x1x2 mm+−33- m + 3 2(12m − 1)(m + 3)− m(m + 3) = − 8m (2m + 1) 24m 2 + 70m − 6− m2 − 3m = − 16m 2 − 8m 2 39m + 75m − 6 = 0 / : 3 13m 2 + 25m − 2 = 0.

Rozwiązujemy otrzymane równanie kwadratowe.

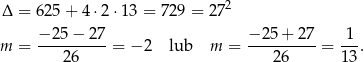
Δ = 625 + 4 ⋅2⋅ 13 = 729 = 272 m = −-25-−-27-= − 2 lub m = −-25-+-27-= 1-. 26 26 13

W tym miejscu łatwo o pomyłkę – zwróćmy uwagę, że jeżeli 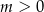m > 0 , to funkcja 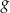g nie przyjmuje wartości największej, więc powyższy rachunek miał sens przy założeniu, że 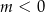m < 0 . W takim razie jedynym rozwiązaniem jest m = − 2 .  
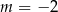Odpowiedź: m = − 2

Wersja PDF