Wykres funkcji f, określonej dla xϵR następującym wzorem... Zadania.info: rozwiązanie zadania, Różne, 8716312

Zaloguj się

Informacje

Zadania

Losowe zadanie

Linki sponsorowane

/Szkoła średnia/Funkcje - wykresy/Parabola/Różne

Zadanie nr 8716312

Wykres funkcji 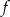$f$ , określonej dla 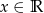$x ∈ R$ następującym wzorem

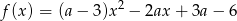
2 f(x) = (a− 3 )x − 2ax + 3a − 6

przecina dodatnią półoś 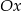$Ox$ w dwóch różnych punktach.

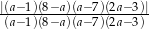Oblicz wartość wyrażenia $|(a−-1)(8−a)(a−7)(2a−3)| (a− 1)(8−a)(a−7)(2a−3)$ .
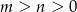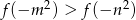Uzasadnij, że dla każdych dwóch liczb rzeczywistych $m > n > 0$ spełniona jest nierówność $2 2 f(−m ) > f(−n )$ .

Rozwiązanie

Zacznijmy od sprawdzenia kiedy funkcja ma dwa miejsca zerowe. Oczywiście musi być kwadratowa (czyli 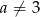$a ⁄= 3$ ) oraz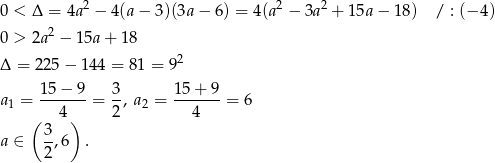 $0 < Δ = 4a2 − 4(a − 3)(3a − 6) = 4(a 2 − 3a 2 + 15a − 1 8) / : (− 4) 2 0 > 2a − 15a + 18 2 Δ = 225− 144 = 81 = 9 15-−-9- 3- 1-5+--9 a1 = 4 = 2, a2 = 4 = 6 ( 3 ) a ∈ -,6 . 2$
Teraz sprawdzamy kiedy oba pierwiastki są dodatnie (korzystamy ze wzorów Viète’a).
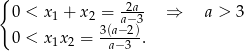
${ 0 < x1 + x2 = -2a- ⇒ a > 3 3(aa−−2)3 0 < x1x2 = -a−3-.$
W pierwszej nierówności skorzystaliśmy z tego, że już wiemy, że musi być 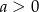$a > 0$ . Druga nierówność jest zawsze spełniona dla 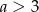$a > 3$ (co wynika z pierwszej nierówności).
Wiemy zatem, że równanie 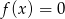$f(x ) = 0$ ma dwa dodatnie pierwiastki dla 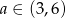$a ∈ (3,6)$ , co pozwala nam ustalić znak każdego z nawiasów w podanym wyrażeniu. Mamy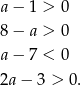
$a − 1 > 0 8 − a > 0 a − 7 < 0 2a − 3 > 0 .$
Zatem podane wyrażenie jest równe
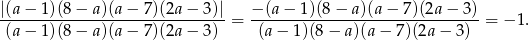
$|(a-−-1)(8-−-a)(a-−-7)(2a-−-3)| = −-(a−--1)(8−--a)(a−--7)(2a−--3)-= − 1. (a − 1)(8 − a)(a − 7)(2a − 3) (a− 1)(8− a)(a− 7)(2a− 3)$

Odpowiedź: -1
Sposób I

Podaną nierówność należy czytać następująco: funkcja 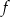$f$ jest malejąca dla 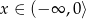$x ∈ (− ∞ ,0⟩$ . Aby sprawdzić czy tak jest liczymy pierwszą współrzędną wierzchołka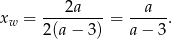
$2a a xw = 2(a−--3)-= a−-3-.$
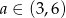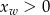Z poprzedniego podpunktu wiemy, że $a ∈ (3,6)$ więc $xw > 0$ . Ponadto ramiona paraboli są skierowane do góry, więc istotnie funkcja 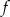$f$ jest malejąca na lewo od 0.

Sposób II

Zamiast zauważać różne rzeczy, możemy też spróbować to wyliczyć.
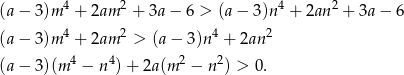
$4 2 4 2 (a− 3)m + 2am + 3a − 6 > (a− 3)n + 2an + 3a − 6 (a− 3)m 4 + 2am 2 > (a− 3)n4 + 2an2 4 4 2 2 (a− 3)(m − n )+ 2a (m − n ) > 0.$
Oba składniki są dodatnie, więc nierówność jest spełniona.