Zadanie nr 1030631
Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:
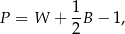
gdzie 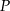 oznacza pole wielokąta,
oznacza pole wielokąta, 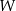 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 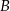 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta.
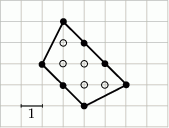
W wielokącie przedstawionym na rysunku 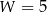 oraz
oraz 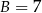 , zatem
, zatem 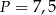 .
.
Wewnątrz pewnego wielokąta znajduje się 6 razy mniej punktów kratowych, niż na jego brzegu. Pole tego wielokąta może być równe
A) 2018 B) 2019 C) 2020 D) 2021
Rozwiązanie
Jeżeli wewnątrz wielokąta jest 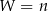 punktów kratowych, to na jego brzegu jest ich
punktów kratowych, to na jego brzegu jest ich 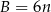 i pole tego wielokąta jest równe
i pole tego wielokąta jest równe
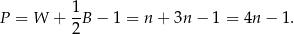
Spośród podanych odpowiedzi, tylko
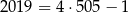
jest liczbą tej postaci.
Odpowiedź: B

