/Szkoła podstawowa/Zadania testowe/Figury przestrzenne/Kula, stożek, walec

Zadanie nr 4548245

Drewniany stożek przecięto na dwie części płaszczyzną równoległą do podstawy i przechodzącą przez środek wysokości stożka.

PIC

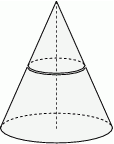
Oceń prawdziwość podanych zdań.

Stosunek masy dolnej części do masy górnej części jest równy 7 PF
Pole powierzchni bocznej górnej części jest 3 razy mniejsze od pola powierzchni bocznej całego stożka. PF
Wersja PDF

Rozwiązanie

Sposób I

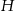Oznaczmy promień podstawy dużego stożka przez r , jego wysokość przez H , a długość tworzącej przez 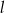l . Objętość i pole powierzchni bocznej dużego stożka są więc równe

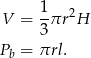
V = 1-πr2H 3 Pb = πrl.

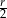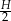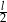Promień podstawy, wysokość i tworząca małego stożka (górnej części) to odpowiednio r 2 , H- 2 i l 2 . Zatem jego objętość i pole powierzchni bocznej są równe

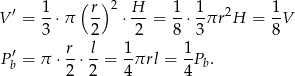
( )2 V ′ = 1⋅ π r- ⋅ H- = 1-⋅ 1πr 2H = 1V 3 2 2 8 3 8 ′ r- l- 1- 1- Pb = π ⋅ 2 ⋅2 = 4πrl = 4Pb .

Objętość dolnej części jest więc równa

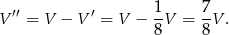
V ′′ = V − V ′ = V − 1-V = 7V . 8 8

Interesujący nas stosunek objętości (a więc też mas) jest równy

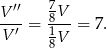
V′′ 78-V- V ′ = 1 V = 7. 8

Sposób II

Górna z otrzymanych części jest stożkiem dwa razy mniejszym od wyjściowego stożka. Jej objętość stanowi więc 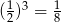1 3 1 (2) = 8 objętości dużego stożka. Objętość dolnej części stanowi więc 78 objętości dużego stożka i interesujący nas stosunek objętości (mas) jest równy

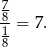
78- 1 = 7. 8

Z tego samego powodu, pole powierzchni bocznej górnego stożka stanowi 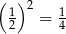( ) 1 2 = 1 2 4 pola powierzchni całego stożka.  
Odpowiedź: P, F

Wersja PDF