Zadanie nr 7114431
Liczby naturalne od 1 do 8 umieszczono w wierzchołkach sześcianu w ten sposób, że w żadnych dwóch wierzchołkach nie umieszczono tej samej liczby. Następnie na każdej krawędzi sześcianu umieszczono sumę liczb, które znajdują się na końcach tej krawędzi, a na środku każdej ściany umieszczono sumę liczb, które znajdują w wierzchołkach tej ściany. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Suma wszystkich liczb umieszczonych na krawędziach sześcianu jest równa 72. | P | F |
| Suma wszystkich liczb umieszczonych w środkach ścian sześcianu jest równa 144. | P | F |
Rozwiązanie
Sposób I
Nie wiemy dokładnie jak zostały umieszczone liczby w wierzchołkach sześcianu, ale każdy wierzchołek jest końcem 3 krawędzi, więc suma wszystkich liczb na krawędziach sześcianu jest 3 razy większa od sumy liczb w wierzchołkach. Jest więc równa
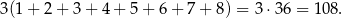
Każdy wierzchołek jest wierzchołkiem trzech ścian sześcianu, więc suma wszystkich liczb napisanych na ścianach sześcianu jest 3 razy większa od sumy liczb w wierzchołkach, więc też jest równa 108.
Sposób II
Szkicujemy sześcian i wykonujemy procedurę opisaną w treści zadania (w jakikolwiek sposób).
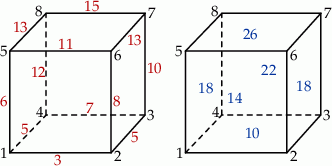
Przy takiej przykładowej konfiguracji łatwo sprawdzić, że obie sumy są równe 108.
Odpowiedź: F, F

