Zadanie nr 1919543
Wielomian 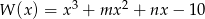 ma trzy pierwiastki
ma trzy pierwiastki 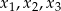 , przy czym
, przy czym 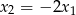 i
i 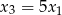 . Wyznacz
. Wyznacz 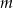 i
i  .
.
Rozwiązanie
Sposób I
Jeżeli pierwiastkami wielomianu 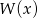 są liczby
są liczby 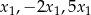 to musi on mieć postać
to musi on mieć postać
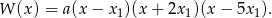
Mamy w takim razie równość
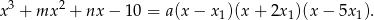
Z prawej strony po wymnożeniu współczynnik przy 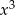 będzie równy
będzie równy  , więc musi być
, więc musi być 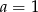 . Pozostaje więc równość
. Pozostaje więc równość
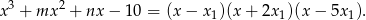
Wymnażamy teraz prawą stronę
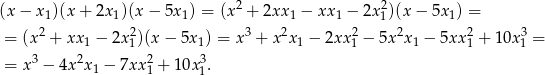
Mamy zatem
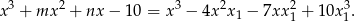
Porównując wyrazy wolne otrzymujemy 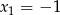 . Wtedy porównując współczynniki przy
. Wtedy porównując współczynniki przy 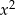 i
i  otrzymujemy
otrzymujemy 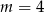 i
i 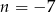 .
.
Sposób II
Korzystamy ze wzorów Viète’a dla równania
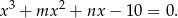
Mają one postać
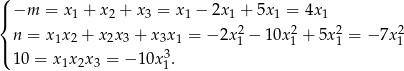
Z trzeciego równania mamy 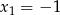 , wtedy z dwóch poprzednich równań
, wtedy z dwóch poprzednich równań 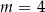 i
i 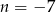 .
.
Odpowiedź: