/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 2960093

Dodaj do ulubionych
Dodaj do rozwiązanych

Wiedząc, że suma kwadratów pierwiastków równania

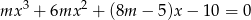
3 2 mx + 6mx + (8m − 5 )x − 10 = 0

jest równa 30, wyznacz 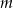m .

Rozwiązanie

Sposób I

Spróbujmy przez chwilę nie przejmować się podanym warunkiem i normalnie sprawdźmy, czy podane równanie nie ma przypadkiem pierwiastka wymiernego. Sprawdzając dzielniki wyrazu wolnego znajdujemy pierwiastek 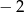− 2 . Dzielimy więc podany wielomian przez 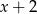x + 2 . My zrobimy to grupując wyrazy.

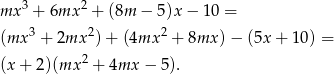
mx 3 + 6mx 2 + (8m − 5)x− 10 = (mx 3 + 2mx 2) + (4mx 2 + 8mx ) − (5x + 10) = 2 (x + 2)(mx + 4mx − 5).

Z podanej informacji o sumie kwadratów pierwiastków wiemy, że suma kwadratów pierwiastków otrzymanego równania kwadratowego wynosi 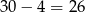30 − 4 = 26 . Korzystając ze wzorów Viète’a mamy

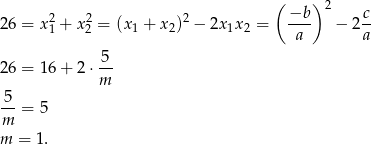
( ) 2 2 2 −b 2 c 26 = x1 + x2 = (x 1 + x 2) − 2x 1x2 = ---- − 2-- a a 26 = 16 + 2 ⋅ 5 m 5 --= 5 m m = 1.

Możemy sprawdzić (choć nie musimy), że dla 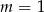m = 1 podane równanie kwadratowe ma pierwiastki 1 i -5.

Sposób II

Okazuje się, że podobnie jak dla równania kwadratowego, istnieją wzory Viète’a dla równań wyższych stopni. Dla równania stopnia 3 mają one postać

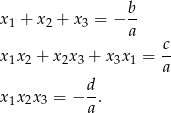
b x1 + x2 + x3 = − -- a c x1x 2 + x 2x3 + x3x1 =-- a d- x1x 2x3 = − a .

gdzie 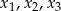x1,x2,x 3 są pierwiastkami równania 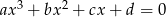ax 3 + bx2 + cx+ d = 0 . Wzory te łatwo uzasadnić porównując współczynniki po obu stronach równości

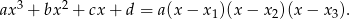
3 2 ax + bx + cx + d = a(x− x1)(x − x2)(x − x3).

Na mocy tych wzorów mamy

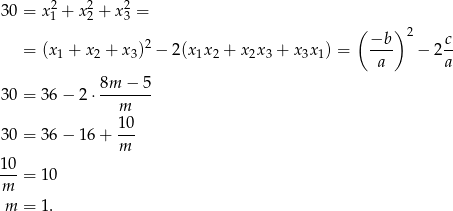
2 2 2 30 = x1 + x2 + x3 = ( ) 2 −b 2 c = (x1 + x2 + x3) − 2(x1x2 + x2x3 + x3x 1) = ---- − 2 -- a a 8m-−--5 30 = 36− 2⋅ m 10 30 = 36− 16 + --- m 10-= 10 m m = 1.

 
Odpowiedź: m = 1

Wersja PDF