Zadanie nr 3037358
Wyznacz wszystkie wartości parametru 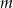 , dla których jedynym rozwiązaniem rzeczywistym równania
, dla których jedynym rozwiązaniem rzeczywistym równania 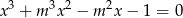 jest liczba 1.
jest liczba 1.
Rozwiązanie
Sposob I
Po pierwsze sprawdzamy, kiedy 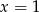 jest rzeczywiście pierwiastkiem podanego wielomianu.
jest rzeczywiście pierwiastkiem podanego wielomianu.

Widzimy zatem, że 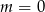 lub
lub 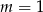 . Dla
. Dla 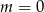 mamy wielomian
mamy wielomian
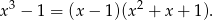
Łatwo sprawdzić (z 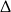 -y), że wielomian w nawiasie nie ma pierwiastków, czyli
-y), że wielomian w nawiasie nie ma pierwiastków, czyli 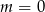 jest ok.
jest ok.
Dla 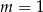 mamy wielomian
mamy wielomian
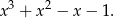
W tym miejscu mamy wiele możliwości, możemy go podzielić przez  , możemy sprawdzić, że drugi dzielnik wyrazu wolnego, czyli -1 też jest pierwiastkiem, możemy wreszcie rozłożyć wielomian bezpośrednio
, możemy sprawdzić, że drugi dzielnik wyrazu wolnego, czyli -1 też jest pierwiastkiem, możemy wreszcie rozłożyć wielomian bezpośrednio
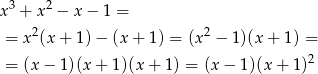
Tak czy inaczej, 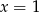 nie jest jedynym pierwiastkiem.
nie jest jedynym pierwiastkiem.
Sposób II
Dzielimy z resztą podany wielomian przez 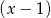 (na razie nie należy przejmować się parametrem
(na razie nie należy przejmować się parametrem 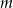 ). Tak jak poprzednio robimy to grupując wyrazy (chociaż najprościej byłoby schematem Hornera):
). Tak jak poprzednio robimy to grupując wyrazy (chociaż najprościej byłoby schematem Hornera):
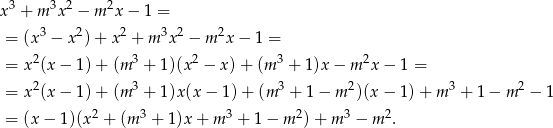
Widać teraz, że 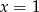 jest pierwiastkiem tylko wtedy, gdy reszta
jest pierwiastkiem tylko wtedy, gdy reszta 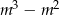 jest równa 0, czyli dla
jest równa 0, czyli dla 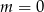 lub
lub 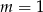 .
.
Dla 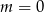 , z powyższego dzielenia mamy:
, z powyższego dzielenia mamy:
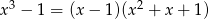
i wielomian 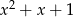 nie ma pierwisatków.
nie ma pierwisatków.
Dla 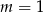 mamy
mamy
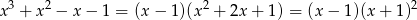
i 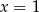 nie jest jedynym pierwiastkiem.
nie jest jedynym pierwiastkiem.
Odpowiedź: