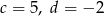Zadanie nr 4040034
Wyznacz współczynniki  i
i 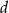 wielomianu
wielomianu 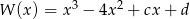 wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu
wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu  .
.
Rozwiązanie
Ponieważ 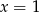 jest pierwiastkiem, mamy
jest pierwiastkiem, mamy
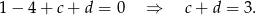
Pozostało teraz wykorzystać informację, że 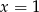 jest pierwiastkiem podwójnym.
jest pierwiastkiem podwójnym.
Sposób I
Najprostszy sposób to użycie pochodnych. Łatwo uzasadnić, że liczba jest pierwiastkiem wielokrotnym wielomianu to jest też pierwiastkiem pochodnej. W naszej sytuacji
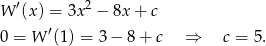
Zatem 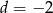 (bo
(bo 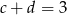 ).
).
Sposób II
Jeżeli nie chcemy używać pochodnych to dzielimy 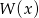 przez
przez 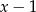 . My zrobimy to grupując wyrazy
. My zrobimy to grupując wyrazy
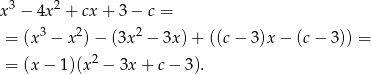
Skoro pierwiastek 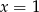 jest dwukrotny to musi być pierwiastkiem otrzymanego wielomianu stopnia 3. Zatem
jest dwukrotny to musi być pierwiastkiem otrzymanego wielomianu stopnia 3. Zatem
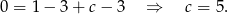
Stąd 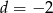 .
.
Sposób III
W zasadzie robimy to co w sposobie II, ale od razu dzielimy przez 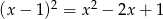 . Sprawdzimy kiedy reszta przy tym dzielniu jest 0.
. Sprawdzimy kiedy reszta przy tym dzielniu jest 0.
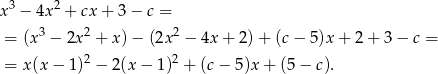
Jeżeli reszta ma być 0, to musi być 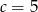 , stąd
, stąd 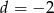 .
.
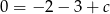
Sposób IV
Jeżeli 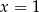 jest pierwiastkiem podwójnym danego wielomianu to musi on mieć postać
jest pierwiastkiem podwójnym danego wielomianu to musi on mieć postać
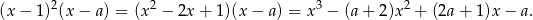
dla pewnego  . Z równości
. Z równości
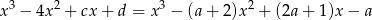
otrzymujemy 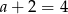 , czyli
, czyli 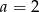 . Zatem
. Zatem
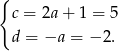
Sposób V
Jeżeli równanie stopnia 3 ma pierwiastek podwójny, to automatycznie ma też trzeci pierwiastek (bo musi to być równanie postaci: 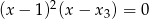 ). W takim razie możemy skorzystać ze wzorów Viète’a dla równania stopnia 3. Mamy zatem
). W takim razie możemy skorzystać ze wzorów Viète’a dla równania stopnia 3. Mamy zatem
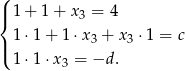
Z pierwszego równania mamy 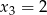 , wtedy drugiego i trzeciego
, wtedy drugiego i trzeciego
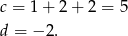
Odpowiedź: